题目内容
已知△ABC,下列条件:①∠A+∠B=∠C,②∠A=∠B= ∠C;③∠A=90°-∠C;④∠A-∠B=90°,可以判定为直角三角形的条件有
∠C;③∠A=90°-∠C;④∠A-∠B=90°,可以判定为直角三角形的条件有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:根据三角形内角和定理及直角三角形的性质对各小题进行逐一判断即可.
解答:①∵△ABC中,∠A+∠B=∠C,∴2∠C=180°,∴∠C=90°,∴此三角形是直角三角形,故本小题正确;
②设∠A=∠B=x,则∠C=2x,∵∠A+∠B+∠C=180°,x+x+2x=180°,解得x=45°,2x=90°,∴此三角形是直角三角形,故本小题正确;
③∵∠A=90°-∠C,∴∠A+∠C=90°,∵∠A+∠B+∠C=180°,∴∠B=180°-(∠A+∠C)=90°,,∴此三角形是直角三角形,故本小题正确;
④∵∠A-∠B=90°,∴∠A>90°,∴△ABC是钝角三角形,故本小题错误.
故选C.
点评:本题考查的是三角形内角和定理及直角三角形的性质,熟知三角形的内角和是180°是解答此题的关键.
分析:根据三角形内角和定理及直角三角形的性质对各小题进行逐一判断即可.
解答:①∵△ABC中,∠A+∠B=∠C,∴2∠C=180°,∴∠C=90°,∴此三角形是直角三角形,故本小题正确;
②设∠A=∠B=x,则∠C=2x,∵∠A+∠B+∠C=180°,x+x+2x=180°,解得x=45°,2x=90°,∴此三角形是直角三角形,故本小题正确;
③∵∠A=90°-∠C,∴∠A+∠C=90°,∵∠A+∠B+∠C=180°,∴∠B=180°-(∠A+∠C)=90°,,∴此三角形是直角三角形,故本小题正确;
④∵∠A-∠B=90°,∴∠A>90°,∴△ABC是钝角三角形,故本小题错误.
故选C.
点评:本题考查的是三角形内角和定理及直角三角形的性质,熟知三角形的内角和是180°是解答此题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目

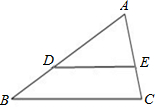 (1)已知△ABC中,D、E分别是边AB、AC上的点,∠A=80°,∠C=70°,∠ADE=30°.求证:DE∥BC.
(1)已知△ABC中,D、E分别是边AB、AC上的点,∠A=80°,∠C=70°,∠ADE=30°.求证:DE∥BC.
 如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④CF=CG.其中正确结论的个数( )
如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④CF=CG.其中正确结论的个数( )