题目内容
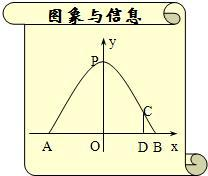
如图所示，已知抛物y=ax2+bx+c与x轴负半轴交于A、B两点，与y轴交于点C，且OB=| 3 |
| 3 |
分析：先根据勾股定理得到OC=3，则B点坐标为（-
，0），C点坐标为（0，3），利用含30°的直角三角形三边的关系得到OA=
OC=3
，则A点坐标为（-3
，0），然后设抛物线的交点式为y=a（x+3
）（x+
），把C（0，3）代入可求得a=
，则抛物线的解析式为y=
（x+3
）（x+
）=
x2+
x+3；然后配成顶点式为y=
（x+2
）2，-1，即可得到抛物线的顶点坐标为（-2
，-1）．
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
解答：解：连BC，如图，
∵OB=
，CB=2
，
∴OC=
=3，
∴B点坐标为（-
，0），C点坐标为（0，3）
在Rt△AOC中，∠CAO=30°，
∴OA=
OC=3
，
∴A点坐标为（-3
，0），
设抛物线的解析式为y=a（x+3
）（x+
），
把C（0，3）代入得a（0+3
）（0+
）=3，
∴a=
，
∴抛物线的解析式为y=
（x+3
）（x+
）=
x2+
x+3；
∵y=
（x+2
）2-1，
∴抛物线的顶点坐标为（-2
，-1）．
∵OB=
| 3 |
| 3 |
∴OC=
| BC2-OB2 |
∴B点坐标为（-
| 3 |
在Rt△AOC中，∠CAO=30°，
∴OA=
| 3 |
| 3 |
∴A点坐标为（-3
| 3 |
设抛物线的解析式为y=a（x+3
| 3 |
| 3 |
把C（0，3）代入得a（0+3
| 3 |
| 3 |
∴a=
| 1 |
| 3 |
∴抛物线的解析式为y=
| 1 |
| 3 |
| 3 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 3 |
∵y=
| 1 |
| 3 |
| 3 |
∴抛物线的顶点坐标为（-2
| 3 |
点评：本题考查了抛物线的交点式：若抛物线与x轴的交点坐标为（x1，0）、（x2，0），则抛物线的解析式为y=a（x-x1）（x-x2）．也考查了含30°的直角三角形三边的关系以及抛物线的顶点式．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
，垂直地面立起一根1.7m长的木杆，其顶端恰好顶在抛物线形门上C处，建立如图所示的坐标系．
一块边缘呈抛物线型的铁片如图放置，测得AB=20cm，抛物线的顶点到AB边的距离为25cm．现要沿AB边向上依次截取宽度均为4cm的矩形铁皮，如图所示．已知截得的铁皮中有一块是正方形，则这块正方形铁皮是（ ）
如图所示，已知抛物y=ax2+bx+c与x轴负半轴交于A、B两点，与y轴交于点C，且OB=
，CB=
，∠CAO=30°，求抛物线的解析式和它的顶点坐标．