题目内容
解答题
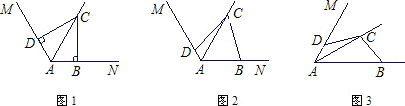
①已知:如图,在△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足.求:AD的长.
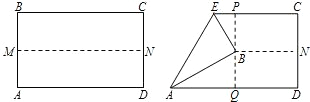
②如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?

①已知:如图,在△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足.求:AD的长.

②如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?

分析:①过C作CE⊥BE交BA的延长线于E,求出∠ACE=30°,求出AE,CE,根据三角形面积公式得出AB×CE=CB×AD,代入求出即可;
②根据题意画出P点的位置,得出A、C关于小河对称,求出BO、CO,根据勾股定理求出BC,即可求出答案.
②根据题意画出P点的位置,得出A、C关于小河对称,求出BO、CO,根据勾股定理求出BC,即可求出答案.
解答:①解:过C作CE⊥BA交BA的延长线于E,
∵∠CAB=120°,
∴∠CAE=60°,
∴∠ACE=30°
∵AC=2,
∴AE=
AC=1
∵在Rt△ACE中,由勾股定理可得:CE2=AC2-AE2=3,
∴CE=
,
在Rt△BCE中,由勾股定理可得:BC2=CE2+BE2=28,
∴BC=2
∵S△ABC=
AB×CE=
CB×AD,
∴
×4×
=
×2
×AD,
∴AD=
;
②解: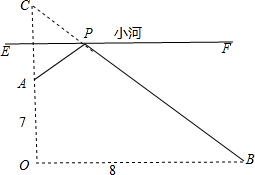
作A关于小河(EF)的对称点C,连接BC交EF于P,则此时AP+BP最小,
过B作OB⊥AC于O,
则BO=8,CA=4+4=8,CO=8+7=15,
则PA+PB=PC+PB=BC=
=17(km),
答:要完成这件事情所走的最短路程是17km.

∵∠CAB=120°,
∴∠CAE=60°,
∴∠ACE=30°
∵AC=2,
∴AE=
| 1 |
| 2 |
∵在Rt△ACE中,由勾股定理可得:CE2=AC2-AE2=3,
∴CE=
| 3 |
在Rt△BCE中,由勾股定理可得:BC2=CE2+BE2=28,
∴BC=2
| 7 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 7 |
∴AD=
| 2 |
| 7 |
| 21 |
②解:

作A关于小河(EF)的对称点C,连接BC交EF于P,则此时AP+BP最小,
过B作OB⊥AC于O,
则BO=8,CA=4+4=8,CO=8+7=15,
则PA+PB=PC+PB=BC=
| 152+82 |
答:要完成这件事情所走的最短路程是17km.
点评:本题考查了勾股定理、轴对称-最短路线问题、含30度角的直角三角形的应用,解(1)的关键是得出关系式AB×CE=CB×AD和求出CB、CE的长,解(2)的关键是找出P点的位置.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目