题目内容
【题目】如图，在四边形ABCD中，
，
，
，
，
，动点M从点B出发沿线段BC以每秒2个单位长度的速度向终点C运动，动点N同时从点C出发沿线段CD以每秒1个单位长度的速度向终点D运动．
设运动的时间为t秒
．
求BC的长．
当
时，求t的值．
设
的面积为
，试确定与t的函数关系式．
在运动过程中，是否存在某一时刻t，使：
：65？若存在，求出t的值；若不存在，请说明理由．
【答案】（1）10； （2）
； （3）
； （4）存在这样的t，其值为2或
；理由见解析.
【解析】
（1）如图①，过A、D分别作
于K，
于H，然后分别求出BK，KH，CH的长即可；
（2）如图②，过D作
交BC于G点，则四边形ADGB是平行四边形，可得GC=7，
，
，再证明
∽
，根据相似三角形对应边成比例列出关于t的方程求解即可；
（3）如图③，过N作
BC于点G，过D作DF⊥BC与点F，则
∽
，根据相似三角形对应边成比例可得到
，再利用三角形面积公式即可得解；
（4）首先求出四边形ABCD的面积，即可得到△MNC的面积，再代入（3）中的函数关系式求解即可.
如图①，过A、D分别作于K，于H，则四边形ADHK是矩形，
，
在
中，
，
，
在
中，由勾股定理得，
．
；
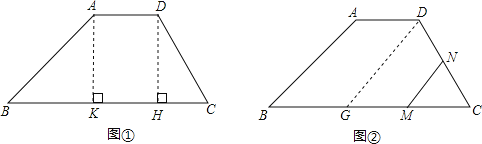
如图②，过D作交BC于G点，则四边形ADGB是平行四边形，
，
，
，
，
由题意知，当M、N运动到t秒时，，，
，
（两直线平行，同位角相等），
又
，
∽，
，即
，
解得：；
如图③，
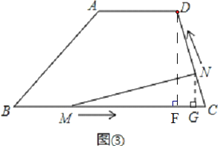
又题意可知，
，
过N作BC于点G，过D作DF⊥BC与点F，
∽，
，即
，
，
；
存在这样的t，其值为2或3；
理由如下：
，
∵
：
：65，
，
代入（3）中得
，
解得：t=2或t=3.
【题目】三台县某中学“五
四”青年节举行了“班班有歌声”歌咏比赛活动比赛聘请了10位教师和10位学生担任评委，其中甲班的得分情况如统计表和统计图．
老师评委评分统计表：
评委序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
分数 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
学生评委评分折线统计图师生评委评分频数分布直方图
补全频数分布直方图．
学生评委评分的中位数是______．
计分办法规定：老师评委、学生评委的评分各去掉一个最高分、一个最低分，并且按教师、学生各占
、
的方法计算各班最后得分，知甲班最后得分
分，试求统计表中的x．
