题目内容
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE
(2)若△BEF也与△ABF相似,请求出 的值 .
的值 .
 |
(1) 在矩形ABCD中,∠A=∠D=90°
 又∵△BCE≌△BFE
又∵△BCE≌△BFE
∴∠BFE=∠A=90° ,∴∠2+∠1=∠DFE°+∠1
∴∠2=∠DFE
△ABF∽△DFE°…(2) 因△BEF也与△ABF相似
∵∠1 =∠4+∠3
∴∠1 ≠∠3…
∴∠2 =∠3
又∵∠3=∠4
∴ ∠2=∠3=∠4=30°
设CE=EF=x,则BC= ,DE=
,DE= ,∴DC=
,∴DC=
 ∴
∴


练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 是方程组
是方程组 的解,则
的解,则 间的关系是( )
间的关系是( ) B.
B. C.
C. D.
D.
 ﹣
﹣ )÷
)÷ ,其中x是方程x2﹣2x=0的根.
,其中x是方程x2﹣2x=0的根.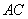 是菱形
是菱形 的对角线,
的对角线, ,则
,则 △BMN :
△BMN : A.
A. B.
B. C.
C. D.
D.
 DC.则图中阴影部分面积为 .
DC.则图中阴影部分面积为 .
 的图象位于 ( )
的图象位于 ( ) 限
限
 馆、桂林大剧院及文化广场,建成后总面积达163500平方米,将成为我市“文化立市”和文化产业大发展的新
馆、桂林大剧院及文化广场,建成后总面积达163500平方米,将成为我市“文化立市”和文化产业大发展的新 标志,把163500平方米用科学记数法可表示为 平方米.
标志,把163500平方米用科学记数法可表示为 平方米.