题目内容
如图(甲)所示,已知点C为线段AB上一点,四边形ACMF和四边形BCNE是两个正方形:如图(乙),若把甲图中的两个正方形换成△ACM、△BCN都是等边三角形.连结DE.
(1)试探究图(甲)中AN与BM的数量关系与位置关系,并说明理由.
(2)求证:AD=ME;(图乙)
(3)求证:DE∥AB; (图乙)
(4)求证:∠BON=60°.(图乙)

(1)试探究图(甲)中AN与BM的数量关系与位置关系,并说明理由.
(2)求证:AD=ME;(图乙)
(3)求证:DE∥AB; (图乙)
(4)求证:∠BON=60°.(图乙)
分析:(1)延长BM交AN于点G,根据正方形的性质就可以得出△BCM≌△NCA,就可以得出AN=BM,∠MGN=90°而得出结论;
(2)先由等边三角形的性质得出△ACN≌△MCB就可以得出∠CMB=∠CAN,再证明△MCE≌△ACD就可以得出结论;
(3)由(2)△MCE≌△ACD可以得出CE=CD,就可以得出△CDE是等边三角形,就可以得出∠DEC=∠NCB而得出结论;
(4)由∠BON=∠AOM=∠NAB+∠ABM=∠CMB+∠CBM=∠ACM而得出结论.
(2)先由等边三角形的性质得出△ACN≌△MCB就可以得出∠CMB=∠CAN,再证明△MCE≌△ACD就可以得出结论;
(3)由(2)△MCE≌△ACD可以得出CE=CD,就可以得出△CDE是等边三角形,就可以得出∠DEC=∠NCB而得出结论;
(4)由∠BON=∠AOM=∠NAB+∠ABM=∠CMB+∠CBM=∠ACM而得出结论.
解答:解:(1)AN=BM,AN⊥BM.
理由:延长BM交AN于点G,
∵四边形ACMF和四边形BCNE是两个正方形,
∴AC=MC,CN=CB,∠ACN=∠MCB=90°.
在△BCM和△NCA中,
,
∴△BCM≌△NCA(SAS),
∴AN=BM,∠ANC=∠MBC.
∵∠MBC+∠CMB=90°,且∠GMN=∠CMB,
∴∠ANC+∠GMN=90°,
∴∠NGM=90°,
∴BG⊥AN,即AN⊥BM.
(2)∵△ACM、△BCN都是等边三角形.
∴∠ACM=∠NCB=60°
∵∠ACM+∠NCB+∠MCN=180°,
∴∠MCN=60°.
∴∠ACM=∠MCN.
∴∠ACM+∠MCN=∠NCB+∠MCN,
∴∠ACN=∠MCB.
在△ACN和△MCB中,
,
∴△ACN≌△MCB(SAS),
∴∠CAN=∠CMB.
在△CAN和△CEM中,
,
∴△CAN≌△CEM(SAS),
∴AD=ME;
(3)∵△CAN≌△CEM,
∴CD=CE.
∵∠MCN=60°,
∴△CDE为等边三角形,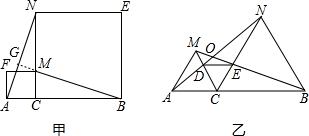
∴∠DEC=60°,
∴∠DEC=∠NCB,
∴DE∥AB;
(4)∵∠BON=∠AOM,且∠AOM=∠NAB+∠ABM,
∴∠BON=∠NAB+∠ABM.
∴∠BON=∠CMB+∠ABM.
∵∠CMB+∠ABM=∠ACM=60°,
∴∠BON=60°.
理由:延长BM交AN于点G,
∵四边形ACMF和四边形BCNE是两个正方形,
∴AC=MC,CN=CB,∠ACN=∠MCB=90°.
在△BCM和△NCA中,
|
∴△BCM≌△NCA(SAS),
∴AN=BM,∠ANC=∠MBC.
∵∠MBC+∠CMB=90°,且∠GMN=∠CMB,
∴∠ANC+∠GMN=90°,
∴∠NGM=90°,
∴BG⊥AN,即AN⊥BM.
(2)∵△ACM、△BCN都是等边三角形.
∴∠ACM=∠NCB=60°
∵∠ACM+∠NCB+∠MCN=180°,
∴∠MCN=60°.
∴∠ACM=∠MCN.
∴∠ACM+∠MCN=∠NCB+∠MCN,
∴∠ACN=∠MCB.
在△ACN和△MCB中,
|
∴△ACN≌△MCB(SAS),
∴∠CAN=∠CMB.
在△CAN和△CEM中,
|
∴△CAN≌△CEM(SAS),
∴AD=ME;
(3)∵△CAN≌△CEM,
∴CD=CE.
∵∠MCN=60°,
∴△CDE为等边三角形,
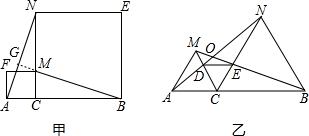
∴∠DEC=60°,
∴∠DEC=∠NCB,
∴DE∥AB;
(4)∵∠BON=∠AOM,且∠AOM=∠NAB+∠ABM,
∴∠BON=∠NAB+∠ABM.
∴∠BON=∠CMB+∠ABM.
∵∠CMB+∠ABM=∠ACM=60°,
∴∠BON=60°.
点评:本题考查了正方形的性质的运用,等边三角形的性质的运用,全等三角形的判定与性质的运用,等边三角形的判定与性质的运用,平行线的判定,三角形的外角与内角的关系的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目

 28、九年级甲、乙两班学生参加电脑知识竞赛,得分均为正整数,将学生成绩进行整理后分成5组,创建频率分布直方图,如图所示,已知图中从左至右的第一、第三、第四、第五小组的频率分别为0.3;0.15;0.1;0.05,且第三小组的频数为6.
28、九年级甲、乙两班学生参加电脑知识竞赛,得分均为正整数,将学生成绩进行整理后分成5组,创建频率分布直方图,如图所示,已知图中从左至右的第一、第三、第四、第五小组的频率分别为0.3;0.15;0.1;0.05,且第三小组的频数为6.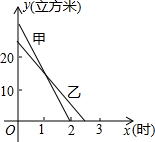 、乙两蓄水池中剩余水量y(立方米)与放水时间x(小时)之间的关系如图所示,已知y乙=-10x+25.
、乙两蓄水池中剩余水量y(立方米)与放水时间x(小时)之间的关系如图所示,已知y乙=-10x+25.