题目内容
【题目】在正方形ABCD中,对角线AC、BD交于点O,点P在线段BC上(不含点B),∠BPE=![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图①):
①求证:△BOG≌△POE;②猜想:![]() = ;
= ;
(2)当点P与点C不重合时,如图②,![]() 的值会改变吗?试说明理由.
的值会改变吗?试说明理由.

【答案】(1)①证明见解析;②![]() ;(2)
;(2)![]() ,不会改变,理由见解析.
,不会改变,理由见解析.
【解析】
(1)①由四边形ABCD是正方形,P与C重合,易证得OB=OP,∠BOC=∠BOG=90°,由同角的余角相等,证得∠GBO=∠EPO,则可利用ASA证得:△BOG≌△POE;
②先判断出∠BPF=∠GPF,进而得出BF=![]() BG,由①得△BOG≌△POE,得出BG=PE,即可得出结论;
BG,由①得△BOG≌△POE,得出BG=PE,即可得出结论;
(2)首先过P作PM∥AC交BG于M,交BO于N,易证得△BMN≌△PEN(ASA),△BPF≌△MPF(ASA),即可得BM=PE,BF=![]() BM.则可求得
BM.则可求得![]()
的值;
(1)①证明:∵四边形ABCD是正方形,P与C重合,
∴OB=OP,∠BOC=∠BOG=90°,
∵PF⊥BG,∠PFB=90°,
∴∠GBO=90°﹣∠BGO,∠EPO=90°﹣∠BGO,
∴∠GBO=∠EPO,
在△BOG和△POE中,
∵ ,
,
∴△BOG≌△POE(ASA);
②由①知,△BOG≌△POE,
∴BG=PE,
∵∠BPE=![]() ∠ACB,∠BPF+∠GPF=∠ACB,
∠ACB,∠BPF+∠GPF=∠ACB,
∴∠BPF=∠GPF,
∵BF⊥PE,
∴BF=![]() BG,
BG,
∴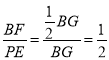 ,
,
故答案为![]() ;
;
(2)解:猜想![]() .
.
证明:如图2,过P作PM∥AC交BG于M,交BO于N,
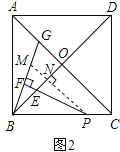
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB=45°,
∴∠NBP=∠NPB.
∴NB=NP.
∵∠MBN=90°﹣∠BMN,∠NPE=90°﹣∠BMN,
∴∠MBN=∠NPE,
在△BMN和△PEN中,
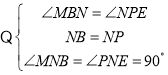 ,
,
∴△BMN≌△PEN(ASA),
∴BM=PE.
∵∠BPE=![]() ∠ACB,∠BPN=∠ACB,
∠ACB,∠BPN=∠ACB,
∴∠BPF=∠MPF.
∵PF⊥BM,
∴∠BFP=∠MFP=90°.
在△BPF和△MPF中,
 ,
,
∴△BPF≌△MPF(ASA).
∴BF=MF.
即BF=![]() BM.
BM.
∴BF=![]() PE.
PE.
即![]() =
=![]() .
.

 名校课堂系列答案
名校课堂系列答案