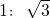Question

一正多边形的一个外角为90°，则它的边心距与半径之比为（　　）

• A、1：2
• B、1：

  2

• C、1：

  3

• D、1：3

Answer 1

分析：利用多边形的外角和是360度，判断该多边形的形状，就很容易求出它的边心距与半径之比了．

解答：解：多边形的外角和是360度，正多边形的一个外角为90°，因而正边形的边数是360÷90=4，因而这个多边形是正方形，因而它的边心距与半径之比为1：

2

．故选B．

点评：根据多边形的外角和定理求多边形的边数是解决本题的关键．