题目内容
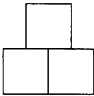 如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为( )
如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:所作最小圆圆心应在对称轴上,且最小圆应尽可能通过圆形的某些顶点,找到对称轴中一点,使其到各顶点的最远距离相等即可求得覆盖本图形最小的圆的圆心,计算半径可解此题.
解答: 解:如图,得
解:如图,得
,
解得:a=
,r=
.
故最小半径为r=
.
故选 D.
 解:如图,得
解:如图,得
|
解得:a=
| 13 |
| 16 |
5
| ||
| 16 |
故最小半径为r=
5
| ||
| 16 |
故选 D.
点评:本题考查了正方形各边相等,且各内角均为直角的性质,考查了勾股定理的运用,本题中构建a、r是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径.
如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径. 如图,用三个边长为a的等边三角形拼成如图(1)所示的等腰梯形,现将这个等腰梯形截成四个全等的等腰梯形(图中的1,2,3,4部分).然后将其中的一个等腰梯形按照上述方法再截成四个全等的等腰梯形.如此重复下去….求第n次截得的一个等腰梯形的周长和面积.
如图,用三个边长为a的等边三角形拼成如图(1)所示的等腰梯形,现将这个等腰梯形截成四个全等的等腰梯形(图中的1,2,3,4部分).然后将其中的一个等腰梯形按照上述方法再截成四个全等的等腰梯形.如此重复下去….求第n次截得的一个等腰梯形的周长和面积.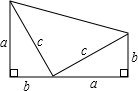 如图:用两个边长为a,b,c的直角三角形拼成一个直角梯形,试用不同的方法计算这个图形的面积,你能发现什么结论?
如图:用两个边长为a,b,c的直角三角形拼成一个直角梯形,试用不同的方法计算这个图形的面积,你能发现什么结论? 如图,用3个边长为1的正方形组成一个对称图形,则能将其完整盖住的圆的最小半径为
如图,用3个边长为1的正方形组成一个对称图形,则能将其完整盖住的圆的最小半径为