题目内容
 如图AB是⊙O的直径,
如图AB是⊙O的直径, 所对的圆心角为60°,
所对的圆心角为60°, 所对的圆心角为20°,且∠AFC=∠BFD,∠AGD=∠BGE,则∠FDG的度数为
所对的圆心角为20°,且∠AFC=∠BFD,∠AGD=∠BGE,则∠FDG的度数为
- A.20°
- B.40°
- C.50°
- D.60°
C
分析:作C关于AB的对称点M,作E关于AB的对称点N,连接CM,FM,求出∠AFM=∠BFD,推出D、F、M三点共线,D、G、N三点共线,求出弧AM=60°,弧BN=20°,即可求出答案.
解答: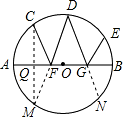 解:作C关于AB的对称点M,作E关于AB的对称点N,连接CM,FM,CM交AB于Q
解:作C关于AB的对称点M,作E关于AB的对称点N,连接CM,FM,CM交AB于Q
则AB⊥CM,CQ=MQ,
∴∠CFA=∠AFM,
∵∠AFC=∠BFD,
∴∠DFB=∠AFM,
即D、F、M三点共线,
同理D、G、N三点共线,
∴弧AC=弧AM=60°,弧BE=弧BN=20°,
∴弧CE=弧MN=180°60°-20°=100°,
∠FDG= 弧MN=50°.
弧MN=50°.
故选C.
点评:本题主要考查对轴对称的性质,垂径定理,圆心角、弧、弦之间的关系,圆周角定理,对顶角等知识点的理解和掌握,能求出弧AM和弧BN的度数是解此题的关键.
分析:作C关于AB的对称点M,作E关于AB的对称点N,连接CM,FM,求出∠AFM=∠BFD,推出D、F、M三点共线,D、G、N三点共线,求出弧AM=60°,弧BN=20°,即可求出答案.
解答:
 解:作C关于AB的对称点M,作E关于AB的对称点N,连接CM,FM,CM交AB于Q
解:作C关于AB的对称点M,作E关于AB的对称点N,连接CM,FM,CM交AB于Q则AB⊥CM,CQ=MQ,
∴∠CFA=∠AFM,
∵∠AFC=∠BFD,
∴∠DFB=∠AFM,
即D、F、M三点共线,
同理D、G、N三点共线,
∴弧AC=弧AM=60°,弧BE=弧BN=20°,
∴弧CE=弧MN=180°60°-20°=100°,
∠FDG=
 弧MN=50°.
弧MN=50°.故选C.
点评:本题主要考查对轴对称的性质,垂径定理,圆心角、弧、弦之间的关系,圆周角定理,对顶角等知识点的理解和掌握,能求出弧AM和弧BN的度数是解此题的关键.

练习册系列答案
相关题目
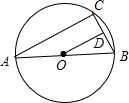 如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
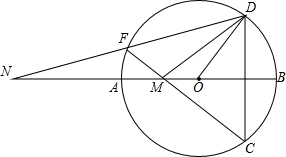 CF交AB于点M,连接DF并延长交BA的延长线于点N.
CF交AB于点M,连接DF并延长交BA的延长线于点N. 如图AB是⊙O的直径,∠D=35°,则∠AOC=
如图AB是⊙O的直径,∠D=35°,则∠AOC= (2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C. (2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.