题目内容
 已知正方形ABCD中,点E在DC边上,DE=4,EC=2,如图,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点间的距离为
已知正方形ABCD中,点E在DC边上,DE=4,EC=2,如图,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点间的距离为4或10
4或10
.分析:分两种情况进行讨论,①当线段AE顺时针旋转时,利用题干条件得到△ADE≌△ABF1,进而得到FC=EC;②当当线段AE逆时针旋转时,利用题干条件得到△ABF2≌△ADE,进而得到F2C=F2B+BC.
解答:解:①当线段AD顺时针旋转得到F1点,
在△ADE和△ABF1中,
,
∴△ADE≌△ABF1,
∴DE=BF1=4,
∴EC=F1C=2;
逆时针旋转得到F2点,同理可得△ABF2≌△ADE,
∴F2B=DE=4,
F2C=F2B+BC=10,
故答案为4或10.

在△ADE和△ABF1中,
|
∴△ADE≌△ABF1,
∴DE=BF1=4,
∴EC=F1C=2;
逆时针旋转得到F2点,同理可得△ABF2≌△ADE,
∴F2B=DE=4,
F2C=F2B+BC=10,
故答案为4或10.
点评:本题主要考查旋转的性质和正方形的性质,解答本题的关键是注意旋转的方向,此题难度不大.

练习册系列答案
相关题目
 如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.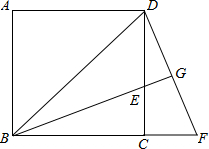 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G. 如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.