МвДїДЪИЭ
ЎѕМвДїЎїМЅѕїМв
ИзНј1Ј¬µИ±ЯЎчABCЦРЈ¬BC=4Ј¬µгPґУµгBіц·ўЈ¬СШBC·ЅПтФЛ¶ЇµЅµгCЈ¬µгP№ШУЪЦ±ПЯABЎўACµД¶ФіЖµг·Ц±рОЄµгMЎўNЈ¬Б¬ЅУMNЈ®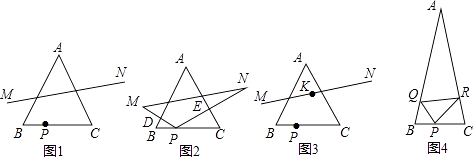
ЈЁ1Ј©Ўѕ·ўПЦЎї
µ±µгPУлµгBЦШєПК±Ј¬ПЯ¶ОMNµДі¤КЗ Ј®
µ±APµДі¤ЧоРЎК±Ј¬ПЯ¶ОMNµДі¤КЗЈ»
ЈЁ2Ј©ЎѕМЅѕїЎї
ИзНј2Ј¬ЙиPB=xЈ¬MN2=yЈ¬Б¬ЅУPMЎўPNЈ¬·Ц±рЅ»ABЈ¬ACУЪµгDЈ¬EЈ®
УГє¬xµДґъКэКЅ±нКѕPM= Ј¬ PN=Ј»
ЈЁ3Ј©Зуy№ШУЪxµДєЇКэ№ШПµКЅЈ¬ІўРґіцyµДИЎЦµ·¶О§Ј»
ЈЁ4Ј©µ±µгPФЪЦ±ПЯBCЙПµДКІГґО»ЦГК±Ј¬ПЯ¶ОMN=3 ![]() ЈЁЦ±ЅУРґіцґр°ёЈ©
ЈЁЦ±ЅУРґіцґр°ёЈ©
ЈЁ5Ј©ЎѕНШХ№Ўї
ИзНј3Ј¬ЗуПЯ¶ОMNµДЦРµгKѕ№эµДВ·ПЯі¤Ј®
ЈЁ6Ј©ЎѕУ¦УГЎї
ИзНј4Ј¬ФЪµИСьЎчABCЦРЈ¬ЎПBAC=30ЎгЈ¬AB=ACЈ¬BC=2Ј¬µгPЎўQЎўR·Ц±рОЄ±ЯBCЎўABЎўACЙПЈЁѕщІ»Ул¶ЛµгЦШєПЈ©µД¶ЇµгЈ¬ФтЎчPQRЦЬі¤µДЧоРЎЦµКЗ Ј®
ЈЁїЙДЬУГµЅµДКэЦµЈєsin75Ўг= ![]() Ј¬cos75Ўг=
Ј¬cos75Ўг= ![]() Ј¬tan75Ўг=2+
Ј¬tan75Ўг=2+ ![]() Ј©
Ј©
Ўѕґр°ёЎї
ЈЁ1Ј©4 ![]() Ј»6
Ј»6
ЈЁ2Ј©![]()
xЈ»![]()
ЈЁ4©ЃxЈ©
ЈЁ3Ј©
ЅвЈє

ИзНј2Ј¬·Ц±р№эµгMЈ¬NЧчЦ±ПЯBCµДґ№ПЯMFЈ¬NGЈ¬ґ№Чг·Ц±рКЗFЈ¬GЈ¬№эµгMЧчMHЎНNGґ№ЧгОЄHЈ®
ЎЯФЪRtЎчPMFЦРЈ¬ЎПMPF=30ЎгЈ¬PM= ![]() xЈ¬
xЈ¬
ЎаMF= ![]() xЈ¬PF=
xЈ¬PF= ![]() xЈ¬
xЈ¬
Н¬АнЈ¬ФЪRtЎчPNGЦРЈ¬ЎПNPG=30ЎгЈ¬PN= ![]() ЈЁ4©ЃxЈ©Ј¬
ЈЁ4©ЃxЈ©Ј¬
ЎаNG= ![]() ЈЁ4©ЃxЈ©Ј¬PG=
ЈЁ4©ЃxЈ©Ј¬PG= ![]() ЈЁ4©ЃxЈ©Ј¬
ЈЁ4©ЃxЈ©Ј¬
ЎЯЛД±ЯРОMFGHКЗѕШРОЈ¬ФтУР
NH=NG©ЃHG=NG©ЃMF= ![]() ЈЁ4©ЃxЈ©©Ѓ
ЈЁ4©ЃxЈ©©Ѓ ![]() x=
x= ![]() ЈЁ2©ЃxЈ©Ј¬
ЈЁ2©ЃxЈ©Ј¬
MH=FG=PF+PG= ![]() x+
x+ ![]() ЈЁ4©ЃxЈ©=6Ј¬
ЈЁ4©ЃxЈ©=6Ј¬
ЎаФЪRtЎчMNHЦРЈ¬УЙ№ґ№Й¶ЁАнµГЈ¬
MN2=NH2+MH2=3ЈЁx©Ѓ2Ј©2+36Ј¬
Фтy=3ЈЁx©Ѓ2Ј©2+36Ј¬
ЎЯ0ЎЬxЎЬ4Ј¬ЗТµ±x=2К±Ј¬yЧоРЎЦµ=36Ј»µ±x=0»т4К±Ј¬yЧоґуЦµ=48Ј¬
Ўа36ЎЬyЎЬ48
ЈЁ4Ј©
ЅвЈєЎЯMN=3 ![]() Ј¬MN2=63Ј¬
Ј¬MN2=63Ј¬
Ўаµ±y=63К±Ј¬јґ3ЈЁx©Ѓ2Ј©2+36=63Ј¬
Ўаx=5»т1Ј¬
Ўаµ±µгPФЪBµгУТІаѕаАлОЄ5Ј¬»тХЯФЪµгPФЪBµгЧуІаѕаАлОЄ1µДО»ЦГґ¦Ј¬ѕщУРПЯ¶ОMN=3 ![]()
ЈЁ5Ј©
ЅвЈєИзНј3Ј¬·Ц±р№эµгMЈ¬NЧчЦ±ПЯBCµДґ№ПЯMFЈ¬NGЈ¬ґ№Чг·Ц±рКЗFЈ¬GЈ¬Б¬ЅУMGЈ¬№эMNµДЦРµгKЈ¬ЧчKTЎНBCУЪµгTЈ¬Ѕ»MGУЪµгSЈ®
ЎЯMFЎОKTЎОNGЈ¬ЗТµгKОЄMNµДЦРµгЈ¬
ЎаKSКЗЎчMNGµДЦРО»ПЯЈ¬
STКЗЎчGMFµДЦРО»ПЯЈ¬

ЈЁ6Ј©2+ ![]()
ЎѕЅвОцЎїЅвЈєЎѕ·ўПЦЎїµ±APµДі¤ЧоРЎК±Ј¬APЎНBCЈ¬јґµгPОЄBCµДЦРµгК±Ј¬
ґЛК±EЎўF·Ц±рОЄABЎўACµДЦРµгЈ¬
ЎаPE= ![]() ACЈ¬PF=
ACЈ¬PF= ![]() ABЈ¬EF=
ABЈ¬EF= ![]() BCЈ¬
BCЈ¬
ЎаMN=ME+EF+FN=PE+EF+PF=6Ј»
µ±µгPєНµгBЦШєПК±Ј¬
ґЛК±GЈЁHЈ©ОЄABЈЁACЈ©µДЦРµгЈ¬
ЎаCG=2 ![]() BH=2
BH=2 ![]() Ј¬
Ј¬
BN=4 ![]() Ј»
Ј»
ЛщТФґр°ёКЗЈє4 ![]() Ј¬6Ј»
Ј¬6Ј»
ЎѕМЅѕїЎїPM=2PD=2ЎБ ![]() PB=
PB= ![]() xЈ¬PN=2PE=2ЎБ
xЈ¬PN=2PE=2ЎБ ![]() PC=2ЎБ
PC=2ЎБ ![]() ЈЁ4©ЃxЈ©=
ЈЁ4©ЃxЈ©= ![]() ЈЁ4©ЃxЈ©Ј»
ЈЁ4©ЃxЈ©Ј»
ЛщТФґр°ёКЗЈє ![]() xЈ¬
xЈ¬ ![]() ЈЁ4©ЃxЈ©Ј»
ЈЁ4©ЃxЈ©Ј»
ЎѕНШХ№Ўї
УЙЎѕМЅѕїЎїЦРµД№эіМїЙЦЄЈ¬ИфЙиPB=xЈ¬ФтУРPC=4©ЃxЈ¬MF= ![]() xЈ¬NG=
xЈ¬NG= ![]() ЈЁ4©ЃxЈ©Ј¬
ЈЁ4©ЃxЈ©Ј¬
УЙИэЅЗРОЦРО»ПЯРФЦКїЙµГЈ¬ST= ![]() MF=
MF= ![]() xЈ¬KS=
xЈ¬KS= ![]() NG=
NG= ![]() ЈЁ4©ЃxЈ©Ј¬
ЈЁ4©ЃxЈ©Ј¬
ЎаKT=ST+KS= ![]() x+
x+ ![]() ЈЁ4©ЃxЈ©=
ЈЁ4©ЃxЈ©= ![]() Ј¬
Ј¬
ТтґЛЈ¬ФЪµгPФЛ¶Ї№эіМЦРЈ¬MNµДЦРµг KµЅBC±ЯѕаАлКјЦХµИУЪ¶ЁЦµ ![]() Ј¬ЗТОЄ
Ј¬ЗТОЄ
µИ±ЯЎчABCёЯµДТ»°лЈ¬ЛщТФMNµДЦРµгKѕ№эµДВ·ПЯЗЎОЄµИ±ЯЎчABCµДЦРО»ПЯЈ¬ЖдВ·ПЯі¤ОЄ2Ј®
ЎѕУ¦УГЎї№эBCµДЦРµгPЧчABЈ¬ACµД¶ФіЖµгMЈ¬NЈ¬Б¬ЅУMNЅ»ABУлQЈ¬Ѕ»ACУЪRЈ¬
ФтґЛК±ЎчPQRЦЬі¤ЧоРЎЈ¬
ЎЯЎПBAC=30ЎгЈ¬
ЎаЎПB=ЎПC=75ЎгЈ¬ЎПMPN=150ЎгЈ¬
ЎаЎПM=ЎПN=15ЎгЈ¬
ЎаЎПMQB=ЎПPQB=ЎПB=75ЎгЈ¬
ЎаMNЎОBCЈ¬PQ=PB=1Ј¬
Н¬АнPR=PC=1Ј¬
ЎЯAPЎНBCЈ¬
ЎаAPЎНMNЈ®
ЎЯЎПPQR=180Ўг©Ѓ75Ўг©Ѓ75Ўг=30ЎгЈ¬
ЎаQR=2ЎБ ![]() PQ=
PQ= ![]() Ј¬
Ј¬
ЎаЎчPQRЦЬі¤µДЧоРЎЦµКЗ2+ ![]() Ј®
Ј®
ЛщТФґр°ёКЗЈє2+ ![]() Ј®
Ј®

 їЄРДНЬЧґФЄЧчТµПµБРґр°ё
їЄРДНЬЧґФЄЧчТµПµБРґр°ё їОК±ХЖїШЛжМГБ·П°ПµБРґр°ё
їОК±ХЖїШЛжМГБ·П°ПµБРґр°ё Т»їОТ»Б·Т»±ѕНЁПµБРґр°ё
Т»їОТ»Б·Т»±ѕНЁПµБРґр°ё ХгЅЦ®РЗС§ТµЛ®ЖЅІвКФПµБРґр°ё
ХгЅЦ®РЗС§ТµЛ®ЖЅІвКФПµБРґр°ё



