Question

△ABC中，AB=AC，D为BC的中点，以D为顶点作∠MDN=∠B．

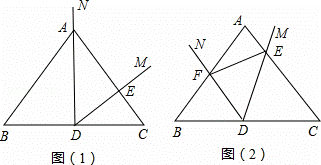
（1）如图（1）当射线DN经过点A时，DM交AC边于点E，不添加辅助线，写出图中所有与△ADE相似的三角形．

（2）如图（2），将∠MDN绕点D沿逆时针方向旋转，DM，DN分别交线段AC，AB于E，F点（点E与点A不重合），不添加辅助线，写出图中所有的相似三角形，并证明你的结论．

（3）在图（2）中，若AB=AC=10，BC=12，当△DEF的面积等于△ABC的面积的时，求线段EF的长．

Answer 1

考点：

相似三角形的判定与性质；等腰三角形的性质；勾股定理；旋转的性质。

专题：

几何综合题。

分析：

（1）根据等腰三角形的性质以及相似三角形的判定得出相似三角形即可；

（2）利用已知首先求出∠BFD=∠CDE，即可得出△BDF∽△CED，再利用相似三角形的性质得出，进而得出△BDF∽△CED∽△DEF．

（3）首先利用△DEF的面积等于△ABC的面积的，求出DH的长，进而利用S_△DEF的值求出EF即可．

解答：

（1）图（1）中与△ADE相似的有△ABD，△ACD，△DCE．

证明：∵AB=AC，D为BC的中点，

∴AD⊥BC，∠B=∠C，∠BAD=∠CAD，

又∵∠MDN=∠B，

∴△ADE∽ABD，

同理可得：△ADE∽△ACD，

∵∠MDN=∠C=∠B，

∠B+∠BAD=90°，∠ADE+∠EDC=90°，

∠B=∠MDN，

∴∠BAD=∠EDC，

∵∠B=∠C，

∴△ABD∽△DCE，

∴△ADE∽△DCE，

（2）△BDF∽△CED∽△DEF，

证明：∵∠B+∠BDF+∠BFD=180°

∠EDF+∠BDF+∠CDE=180°，

又∵∠EDF=∠B，∴∠BFD=∠CDE，

由AB=AC，得∠B=∠C，

∴△BDF∽△CED，

∴．

∵BD=CD，

∴．

又∵∠C=∠EDF，

∴△BDF∽△CED∽△DEF．  

（3）连接AD，过D点作DG⊥EF，DH⊥BF，垂足分别为G，H．

∵AB=AC，D是BC的中点，

∴AD⊥BC，BD=BC=6．

在Rt△ABD中，AD²=AB²﹣BD²，

∴AD=8

∴S_△ABC=BC•AD=×12×8=48．

S_△DEF=S_△ABC=×48=12．

又∵AD•BD=AB．DH，

∴DH===，

∵△BDF∽△DEF，

∴∠DFB=∠EFD  

∵DG⊥EF，DH⊥BF，

∴DH=DG=．

∵S_△DEF=×EF×DG=12，

∴EF==5．

点评：

此题主要考查了相似三角形判定与性质以及三角形面积计算，熟练应用相似三角形的性质与判定得出对应用边与对应角的关系是解题关键．