题目内容
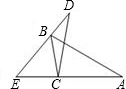 如图,△ABC≌△DEC,∠A:∠ABC:∠BCA=3:5:10,
如图,△ABC≌△DEC,∠A:∠ABC:∠BCA=3:5:10,
(1)求∠D的度数;
(2)求∠EBC的度数.
解:(1)∵∠A+∠ABC+∠BCA=180°,∠A:∠ABC:∠BCA=3:5:10,
∴∠A=180°×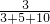 =30°,∠ABC=180°×
=30°,∠ABC=180°×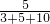 =50°,∠BCA=180°×
=50°,∠BCA=180°× =100°,
=100°,
又∵△ABC≌△DEC,
∴∠D=∠A=30°;
(2)∵△ABC≌△DEC,
∴∠E=∠ABC=50°,
∵∠BCA=100°,
∴∠EBC=∠BCA-∠E,
=100°-50°=50°.
分析:(1)根据三角形内角和等于180°,再根据比值求出△ABC的各内角的度数,再根据全等三角形对应角相等即可求出∠D的度数;
(2)先根据全等三角形对应角相等求出∠E=∠ABC=50°,再根据三角形的一个外角等于和它不相邻的两个内角的和解答.
点评:本题主要利用全等三角形对应角相等的性质和三角形的一个外角等于和它不相邻的两个内角的和的性质,熟练掌握性质是解题的关键.
∴∠A=180°×
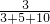 =30°,∠ABC=180°×
=30°,∠ABC=180°×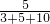 =50°,∠BCA=180°×
=50°,∠BCA=180°× =100°,
=100°,又∵△ABC≌△DEC,
∴∠D=∠A=30°;
(2)∵△ABC≌△DEC,
∴∠E=∠ABC=50°,
∵∠BCA=100°,
∴∠EBC=∠BCA-∠E,
=100°-50°=50°.
分析:(1)根据三角形内角和等于180°,再根据比值求出△ABC的各内角的度数,再根据全等三角形对应角相等即可求出∠D的度数;
(2)先根据全等三角形对应角相等求出∠E=∠ABC=50°,再根据三角形的一个外角等于和它不相邻的两个内角的和解答.
点评:本题主要利用全等三角形对应角相等的性质和三角形的一个外角等于和它不相邻的两个内角的和的性质,熟练掌握性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
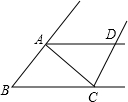 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
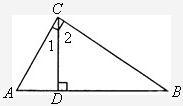
 ,且CB=CE.
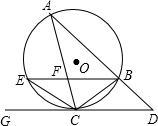
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.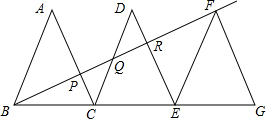 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且