Question

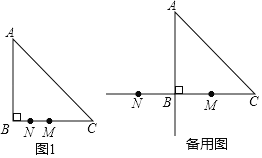
【题目】在△ABC中，∠ABC＝90°，AB＝BC＝2，点M是线段BC的中点，点N在射线MB上，连接AN，平移△ABN，使点N移动到点M，得到△DEM（点D与点A对应，点E与点B对应），DM交AC于点P．

（1）若点N是线段MB的中点，如图1．

①依题意补全图1；

②求DP的长；

（2）若点N在线段MB的延长线上，射线DM与射线AB交于点Q，若MQ＝DP，求CE的长．

Answer 1

【答案】（1）①见解析，②；（2）2﹣2

【解析】

（1）利用平移的性质画出图形，再利用相似得出比例式，即可求出线段DP的长；

（2）根据条件MQ＝DP，利用平行四边形的性质和相似三角形的性质，求出BN的长即可解决．

解：（1）①如图1，补全图形：

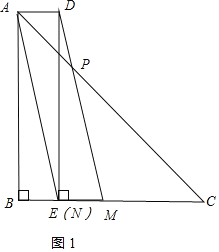
②连接AD，如图1，

在Rt△ABN中，

∵∠B＝90°，AB＝4，BN＝1，

∴AN＝，

∵线段AN平移得到线段DM，

∴DM＝AN＝，

由平移可得，AD＝NM＝1，AD∥MC，

∴△ADP∽△CMP，

∴，

∴DP＝DM＝；

（2）如图2，连接NQ，

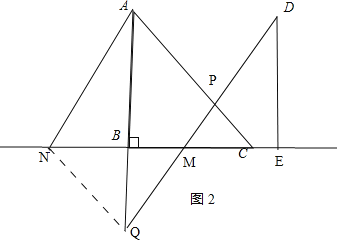
由平移知：AN∥DM，且AN＝DM，

∵MQ＝DP，

∴PQ＝DM，

∴AN∥PQ，且AN＝PQ，

∴四边形ANQP是平行四边形，

∴NQ∥AP，

∴∠BQN＝∠BAC＝45°，

又∵∠NBQ＝∠ABC＝90°，

∴BN＝BQ，

∵AN∥MQ，

∴,

又∵M是BC的中点，且AB＝BC＝4，

∴,

∴NB＝2 或-2 （舍去），

∴ME＝BN＝2，

∴CE＝2﹣2．