题目内容
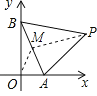
【题目】如图，点P在第一象限，△ABP是边长为2的等边三角形，当点A在x轴的正半轴上运动时，点B随之在y轴的正半轴上运动，运动过程中，点P到原点的最大距离是______；若将△ABP的PA边长改为
，另两边长度不变，则点P到原点的最大距离变为______．
【答案】1+
1+
【解析】
根据当O到AB的距离最大时，OP的值最大，得到O到AB的最大值是
AB=1，此时在斜边的中点M上，由勾股定理求出PM，即可求出答案；将△ABP的PA边长改为
，另两边长度不变，根据
，得到∠PBA=90°，由勾股定理求出PM即可．
取AB的中点M，连OM，PM，
在Rt△ABO中，OM=
=1，在等边三角形ABP中，PM=，
无论△ABP如何运动，OM和PM的大小不变，当OM，PM在一直线上时，P距O最远，
∵O到AB的最大值是AB=1，此时在斜边的中点M上， 由勾股定理得：PM=，
∴OP=1+，
将△AOP的PA边长改为，另两边长度不变， ∵，
∴∠PBA=90°，由勾股定理得：PM=， ∴此时OP=OM+PM=1+．
练习册系列答案
相关题目
【题目】(1)填表：
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律：______________________________.
(3)根据你发现的规律填空：
①已知
=1.442,则
=__________,
=__________；
②已知
=0.076 96,则
=__________.
