题目内容
(2002•湛江)已知关于x的一元二次方程(m+2)x2+2mx+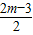 =0.
=0.(1)若方程有两个不相等的实数根,求m的取值范围;
(2)若
 <m<6,试判断方程两个实数根的符号,并证明你的结论.
<m<6,试判断方程两个实数根的符号,并证明你的结论.
【答案】分析:(1)由题意可知:若方程有两个不相等的实数根,则判别式一定>0,则据此可以求得m的取值范围;又因为是一元二次方程,所以二次项系数不能为0,即m+2≠0,则m≠-2;
(2)根据根与系数的关系以及m的取值范围可以确定两个实数根的符号.
解答:解:(1)△=(2m)2-4(m+2)•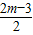 =-2m+12,
=-2m+12,
若方程有不等的实根,则必须使△>0,即-2m+12>0,解得:m<6;
又因为m+2≠0,则m≠-2;所以m的取值范围是m<6且m≠-2;
答:m的取值范围是m<6且m≠-2.
(2)设方程的两个实根分别为α与β,则根据根与系数的关系得:α+β=-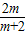 ,α•β=
,α•β=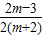 ,
,
又知 <m<6,则-
<m<6,则-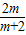 <0,
<0,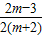 >0;
>0;
即α+β<0,α•β>0;所以方程有两个负实数根.
点评:本题考查了一元二次方程根的判别式的应用.切记不要忽略一元二次方程二次项系数不为零这一隐含条件.
同时还考查了根与系数的关系的应用.
(2)根据根与系数的关系以及m的取值范围可以确定两个实数根的符号.
解答:解:(1)△=(2m)2-4(m+2)•
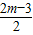 =-2m+12,
=-2m+12,若方程有不等的实根,则必须使△>0,即-2m+12>0,解得:m<6;
又因为m+2≠0,则m≠-2;所以m的取值范围是m<6且m≠-2;
答:m的取值范围是m<6且m≠-2.
(2)设方程的两个实根分别为α与β,则根据根与系数的关系得:α+β=-
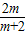 ,α•β=
,α•β=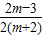 ,
,又知
 <m<6,则-
<m<6,则-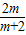 <0,
<0,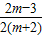 >0;
>0;即α+β<0,α•β>0;所以方程有两个负实数根.
点评:本题考查了一元二次方程根的判别式的应用.切记不要忽略一元二次方程二次项系数不为零这一隐含条件.
同时还考查了根与系数的关系的应用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 =0.
=0. <m<6,试判断方程两个实数根的符号,并证明你的结论.
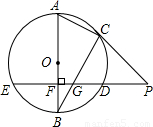
<m<6,试判断方程两个实数根的符号,并证明你的结论.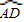 上运动,其他条件不变,问应再具备什么条件可使结论BG2=BF•BO成立?(要求画出示意图并说明理由)
上运动,其他条件不变,问应再具备什么条件可使结论BG2=BF•BO成立?(要求画出示意图并说明理由)