Question

一块含30°角的直角三角板与一块含45°角的直角三角板按如图的方式拼放在一起，其中BC=DC=5cm，等腰直角边ED与斜边AB相交于G，则EG的长是________cm．

Answer 1

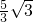
分析：根据两个直角三角形的性质得到GD∥BC，然后利用平行线分线段成比例定理得到=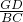，进而求得线段GD的长，然后再利用等腰直角三角形的性质得到ED的长，然后求得线段EG的长即可．
解答：∵∠EDC=∠DCB=90°，
∴ED∥BC，
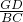∴=E
∵在直角三角形ABC中，BC=CD=5，∠A=30°，
∴AC=BC=5
∴AD=AC-CD=5-5
∴
解得：GD=5-
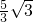
∵∠DEC=∠DCE=45°，
∴ED=DC=5
∴EG=ED-GD=5-（5-）=
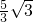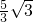
故答案为：
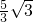
点评：本题考查了相似三角形的判定及性质，解题的关键是利用题目中已有的直角三角形得到相似三角形，并利用相似三角形的性质进行有关的计算．