题目内容
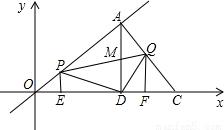
已知:如图,在平面直角坐标系内,直线y= x上有一点A,AD⊥x轴于D,且AD=3,C是x轴上的一点,AC⊥AO,长度等于OD的线段EF在x轴上沿OC方向以1/s的速度向点C运动(运动前EF和OD重合,当F点与C重合时停止运动,包括起点、终点),过E,F分别作OC的垂线交直角边于点P、点Q,连接线段PD,QD,PQ,PQ交线段AD于点M,若设EF运动的时间为t(s).
x上有一点A,AD⊥x轴于D,且AD=3,C是x轴上的一点,AC⊥AO,长度等于OD的线段EF在x轴上沿OC方向以1/s的速度向点C运动(运动前EF和OD重合,当F点与C重合时停止运动,包括起点、终点),过E,F分别作OC的垂线交直角边于点P、点Q,连接线段PD,QD,PQ,PQ交线段AD于点M,若设EF运动的时间为t(s).(1)写出A点坐标______.PE=______(用含t的代数式表示线段),其中自变量t的取值范围为______;
(2)是否存在t的值,使得线段PD⊥QD?若存在,请求出相应的t的值,若不存在,请说明理由;
(3)①当t=
 秒时,线段AM=______;
秒时,线段AM=______;②求线段AM关于自变量t的函数解析式,并求出AM的最大值.
【答案】分析:(1)根据直线方程和点的纵坐标可以求出横坐标,进而求出点的坐标;找到终点位置,可以知道t的极限值.
(2)把结论当做已知条件,根据勾股定理或者三角形相似列出方程式,找到相应的关系式,验证是否在定义域内即可.
(3)可以有多种做法,例如S△APQ面积的多种求法、△PMH∽△PTQ等都可以列出方程式,根据定义域可以知道最大值.
解答:解:(1)∵AD⊥x轴于D,且AD=3点A过直线y= x
x
∴代入函数式解得A点坐标为(4,3)
解法①由题意得P点横坐标为t,过直线y= x,所以纵为坐标
x,所以纵为坐标 ,即PE=
,即PE= ;
;
解法②∵AP⊥AQ,AM⊥EF
易证△AOD∽△ADC∽△AOC∽△OPE∽△CQF,且三边之比都为3:4:5,
求得PE= ,DC=
,DC= .
.
∴t的取值范围为0≤t≤ ;
;
(2)不存在t的值使PD⊥QD,理由如下:
方法一(相似)
∵OE=DF=t,∴FC= -t
-t
∴QF=
若PD⊥QD,易证△PED∽△DQF
则 =
=
∴ =
=
4-t= -t
-t
4=
这是不可能的,
∴不存在t的值使PD⊥QD
方法二(勾股定理的逆定理)
∵AP2+AQ2=(5- )2+(
)2+( )2=25-
)2=25- +
+ 2+
2+ 2(2分)
2(2分)
PD2+QD2=(PE2+DE2)+(DF2+FQ2)=( )2+(4-t)2+t2+(3-
)2+(4-t)2+t2+(3- )2(1分)
)2(1分)
∴AP2+AQ2≠PD2+QD2
∴PD⊥QD不可能(2分)
∴不存在t的值使PD⊥QD.
(3)① 解法如下,只要把当t=
解法如下,只要把当t= 秒代入②中表达式
秒代入②中表达式
②方法一(面积法):
∵AP⊥AQ,AM⊥EF
∴S△APQ= AP×AQ=
AP×AQ= AM×ED+
AM×ED+ AM×DF=
AM×DF= AM×EF
AM×EF
∴AM= =
=
= =-
=- 2
2
=- (t-2)2+
(t-2)2+
∴当t=2秒时,AM最大值为 .
.
方法二(相似)
过P作PH⊥QF于T,交AD于H.
QT=3- -
- =3-
=3-
∵△PMH∽△PTQ
∴ =
=
即 =
=
∴MH=- 2-
2- +3
+3
∴AM=AD-HD-MH=- 2+
2+
∴当t=2秒时,AM最大值为
方法三(函数法)
设直线PQ解析式为y=kx+b.
∵P(t, ),Q(t+4,3-
),Q(t+4,3- )
)
∴ 解得
解得

∴y=( )x+
)x+
∵Mx=4
∴My=( )×4+
)×4+ =3-
=3- =MD
=MD
∴AM=AD-MD
=3-(3- )
)
=- 2+
2+
∴当t=2秒时,AM最大值为 .
.
点评:本题是函数与各种图形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题,在平常的练习中多加注意.每道题都有不同的做法,根据不同的知识点可以有很多种思路,尝试着多种方法做题可以很好的巩固所学知识.
(2)把结论当做已知条件,根据勾股定理或者三角形相似列出方程式,找到相应的关系式,验证是否在定义域内即可.
(3)可以有多种做法,例如S△APQ面积的多种求法、△PMH∽△PTQ等都可以列出方程式,根据定义域可以知道最大值.
解答:解:(1)∵AD⊥x轴于D,且AD=3点A过直线y=
 x
x∴代入函数式解得A点坐标为(4,3)
解法①由题意得P点横坐标为t,过直线y=
 x,所以纵为坐标
x,所以纵为坐标 ,即PE=
,即PE= ;
;解法②∵AP⊥AQ,AM⊥EF
易证△AOD∽△ADC∽△AOC∽△OPE∽△CQF,且三边之比都为3:4:5,
求得PE=
 ,DC=
,DC= .
.∴t的取值范围为0≤t≤
 ;
;(2)不存在t的值使PD⊥QD,理由如下:

方法一(相似)
∵OE=DF=t,∴FC=
 -t
-t∴QF=

若PD⊥QD,易证△PED∽△DQF
则
 =
=
∴
 =
=
4-t=
 -t
-t4=

这是不可能的,
∴不存在t的值使PD⊥QD
方法二(勾股定理的逆定理)
∵AP2+AQ2=(5-
 )2+(
)2+( )2=25-
)2=25- +
+ 2+
2+ 2(2分)
2(2分)PD2+QD2=(PE2+DE2)+(DF2+FQ2)=(
 )2+(4-t)2+t2+(3-
)2+(4-t)2+t2+(3- )2(1分)
)2(1分)∴AP2+AQ2≠PD2+QD2
∴PD⊥QD不可能(2分)
∴不存在t的值使PD⊥QD.
(3)①
 解法如下,只要把当t=
解法如下,只要把当t= 秒代入②中表达式
秒代入②中表达式②方法一(面积法):
∵AP⊥AQ,AM⊥EF
∴S△APQ=
 AP×AQ=
AP×AQ= AM×ED+
AM×ED+ AM×DF=
AM×DF= AM×EF
AM×EF∴AM=
 =
=
=
 =-
=- 2
2=-
 (t-2)2+
(t-2)2+
∴当t=2秒时,AM最大值为
 .
.方法二(相似)
过P作PH⊥QF于T,交AD于H.
QT=3-
 -
- =3-
=3-
∵△PMH∽△PTQ
∴
 =
=
即
 =
=
∴MH=-
 2-
2- +3
+3∴AM=AD-HD-MH=-
 2+
2+
∴当t=2秒时,AM最大值为

方法三(函数法)
设直线PQ解析式为y=kx+b.
∵P(t,
 ),Q(t+4,3-
),Q(t+4,3- )
)∴
 解得
解得

∴y=(
 )x+
)x+
∵Mx=4
∴My=(
 )×4+
)×4+ =3-
=3- =MD
=MD∴AM=AD-MD
=3-(3-
 )
)=-
 2+
2+
∴当t=2秒时,AM最大值为
 .
.点评:本题是函数与各种图形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题,在平常的练习中多加注意.每道题都有不同的做法,根据不同的知识点可以有很多种思路,尝试着多种方法做题可以很好的巩固所学知识.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).

