Question

【题目】如图，已知△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线，交CE的延长线于点F，且AF=BD，连接BF．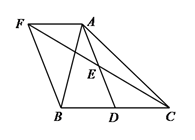

（1）求证：BD=CD；
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．

Answer 1

【答案】
（1）

证明：∵AF∥BC，

∴∠AFE=∠DCE，

∵E是AD的中点，

∴AE=DE，

在△AEF和△DEC中，

∠AFE=∠DCE，∠AEF=∠DEC，AE=DE，

∴△AEF≌△DEC（AAS），

∴AF=CD，

∵AF=BD，

∴BD=CD

（2）

解：当△ABC满足AB=AC时，四边形AFBD是矩形．

理由如下：∵AF∥BD，AF=BD，

∴四边形AFBD是平行四边形，

∵AB=AC，BD=CD，

∴∠ADB=90°，

∴□AFBD是矩形

【解析】根据两直线平行，内错角相等求出∠AFE=∠DCE，然后利用“角角边”证明△AEF和△DEC全等，根据全等三角形对应边相等可得AF=CD，再利用等量代换即可得证；
（2）先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形，再根据一个角是直角的平行四边形是矩形，可知∠ADB=90°，由等腰三角形三线合一的性质可知必须是AB=AC．
【考点精析】认真审题，首先需要了解等腰三角形的性质(等腰三角形的两个底角相等（简称：等边对等角）)，还要掌握平行四边形的判定与性质(若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积)的相关知识才是答题的关键．