题目内容
如果平行四边形ABCD对角线AC与BD交于O,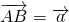 ,
,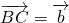 ,那么
,那么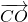 可以用向量
可以用向量 、
、 表示为________.
表示为________.
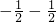
分析:首先由平行四边形的性质得到OC=
 AC,由向量的知识,即可得到
AC,由向量的知识,即可得到 ,则可求得
,则可求得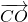 的值.
的值.解答:
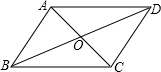 解:如图:
解:如图:∵四边形ABCD是平行四边形,
∴OA=OC=
 AC,
AC,∴
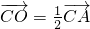 ,
,∵
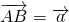 ,
,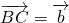 ,
,∴
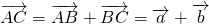 ,
,∴
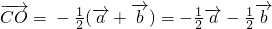 .
.故答案为:-

 -
-
 .
.点评:此题考查向量的知识与平行四边形的性质,解题的关键是注意数形结合思想的应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
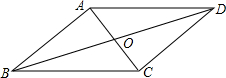 如图,四边形ABCD是平行四边形,对角线AC、BD相交于O.
如图,四边形ABCD是平行四边形,对角线AC、BD相交于O.
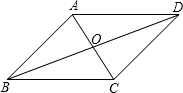 如图,四边形ABCD是平行四边形,对角线AC、BD相交于O.
如图,四边形ABCD是平行四边形,对角线AC、BD相交于O.