Question

【题目】如图，在中，，点是的中点.在和上.分别有一动点，在移动过程中保持.

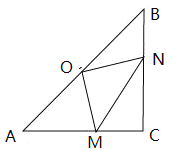
（1）判断的形状，并说明理出.

（2）当时，求四边形的面积.

Answer 1

【答案】（1）等腰直角三角形，见解析；（2）

【解析】

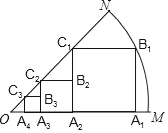
连接OC.先证得△OAM≌△CNO，然后根据全等三角形的对应边相等推知OM=ON；然后由等腰直角三角形ABC的性质、等腰三角形OMN的性质推知∠NOM=90°，即△OMN是等腰直角三角形；

（2）由（1）得△OAM≌△CNO，所以四边形的面积等于△OAC的面积，根据题意可得OC=OA =AB=5，从而求解.

解: (1)是等腰直角三角形.理由如下:

连接.

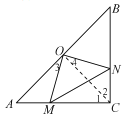
，点是的中点，

(三线合一)

.

.

.

，

.

.

.

是等腰直角三角形.

(2)∵AB=10,∴OC=AB=5=OA,

由(1)，，OC⊥AAB，

.

.