Question

【题目】如图，抛物线y=ax2+bx经过A（2，0），B（3，﹣3）两点，抛物线的顶点为C，动点P在直线OB上方的抛物线上，过点P作直线PM∥y轴，交x轴于M，交OB于N，设点P的横坐标为m．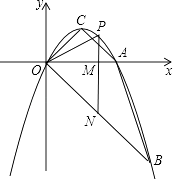

（1）求抛物线的解析式及点C的坐标；
（2）当△PON为等腰三角形时，点N的坐标为；当△PMO∽△COB时，点P的坐标为；（直接写出结果）
（3）直线PN能否将四边形ABOC分为面积比为1：2的两部分？若能，请求出m的值；若不能，请说明理由．

Answer 1

【答案】
（1）

解：根据题意，得 ，解这个方程组得

∴抛物线的解析式为y=﹣x2+2x

当x=﹣ =1时，y=﹣x2+2x=1，

∴C（1，1）

（2）（1，﹣1），（2，﹣2），（3﹣ ， ﹣3）；（ ， ），（ ，﹣ ）
（3）

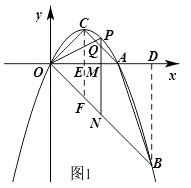
如图1，作BD⊥x轴于D，作CE⊥x轴于E，交OB于F

则BD=OD=3，CE=OE=1，OC=AC

∴△ODB，△OCE，△AOC均为等腰直角三角形，

∴S四边形ABOC=S△OAC+S△OAB= + OABD=4

∴∠AOC=∠AOB=∠OAC=45°

∵PM∥y轴，

∴OM⊥PN，∠MNO=∠AOB=45°，

∴OM=MN=m，OE=EF=1

①∵S△OCF= CFOE=1 ×4

∴当0＜m≤1时，不能满足条件，

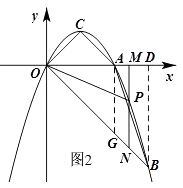
②当1＜m≤2时，如图2，设PN交AC于Q，则MQ=MA=2﹣m，

S四边形OCQN=S△OAC+S△OMN﹣S△AMQ= OACE+ OMMN﹣ AMMQ=2m﹣1，

由S四边形OCQM= S四边形ABOC，得2m﹣1= ×4，解得m= ，

而1＜ ＜2，符合题意，

由S四边形OCQN= S四边形ABOC，得2m﹣1= ，解得m=

而1＜ ＜2，符合题意，

③当2＜m＜3时，如图2，作AG⊥x轴，交OB于G，

则AG=OA=2，AD=1

∴S△ABG= AGAD=1＜ ×4

∴当2＜m＜3时，不能满足条件

∴m= 或m= ．

【解析】（2）①∵B（3，﹣3），
∴直线OB的解析式为y=﹣x，
∵P的横坐标为m（0＜m＜3），
∴P（m，﹣m2+2m），
∴N（m，﹣m），
∴PN2=（﹣m2+3m）2 ， OP2=m2+（﹣m2+2m）2 ， ON2=2m2 ，
当△PON为等腰三角形时，
①当OP=ON时，m2+（﹣m2+2m）2=2m2 ，
∴m=0（舍）或m=1或m=3（舍），
∴N（1，﹣1）
②当OP=PN时，（﹣m2+3m）2=m2+（﹣m2+2m）2 ，
∴m=0（舍）或m=2，
∴N（2，﹣2），
③当ON=PN时，（﹣m2+3m）2=2m2 ，
∴m=0（舍）或m=3+ （舍）或m=3﹣ ，
∴N（3﹣ ， ﹣3），
所以答案是：（1，﹣1），（2，﹣2），（3﹣ ， ﹣3）
②∵P的横坐标为m（0＜m＜3），
∴P（m，﹣m2+2m），
∴M（m，0），
∴PM=|﹣m2+2m|，OM=m，
∵B（3，﹣3），
∴OB=3，
由（1）知，C（1，1），
∴OC=1，
∵△PMO∽△COB，
∴ ，
∴ ，
∴m= 或m= ，
∴P（ ， ）或（ ，﹣ ），
所以答案是：（ ， ），（ ，﹣ ），
【考点精析】利用等腰直角三角形和等腰三角形的性质对题目进行判断即可得到答案，需要熟知等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；等腰三角形的两个底角相等（简称：等边对等角）．