题目内容
【题目】解下列各题（每题5分，共30分）
（1）
（2）
（3）
（4） 解不等式2（x+2）-6≤-5（x-4）
（5）
（6） 
【答案】（1）x=-15；（2）
；（3）－4.5≤x＜1；
（4）x≤
；（5）
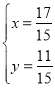；（6）
.
【解析】
（1）根据解一元一次方程的方法步骤求解即可；
（2）用代入消元法或加减消元法求解；
（3）先解每个不等式的解集，再求其公共部分；
（4）根据解一元一次不等式的方法步骤求解；
（5）先化简方程组的两个方程，再用代入消元法或加减消元法求解；
（6）把x=3z代入后两个方程并化简，再解由y、z组成的二元一次方程组，即可求得原方程组的解.
解：（1）去分母得，
去括号得，
，
移项化简得，
，
即
.
（2）
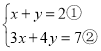，①×4－②，得
，
把代入①得，
，解得y=1，
所以方程组的解是.
（3）
，
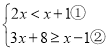解不等式①得，x＜1，
解不等式②得，x≥－4.5，
所以不等式组的解集是－4.5≤x＜1.
（4）2（x+2）－6≤－5（x－4）
去括号得，
移项化简得，
不等式两边同时除以7得，x≤.
（5）原方程组可化为：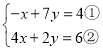
，
①×4+②得，
，解得：
；
把代入①，得
，解得：
.
所以原方程组的解是.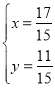
（6）
，
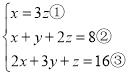把①代入②得，
，即
④，
把①代入③得，
，即
⑤，
解由④⑤组成的方程组得：
，
把z=1代入①得，x=3；
所以原方程组的解是.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
