题目内容
设x,y为正实数,且xy=1.当x=| 1 |
| x4 |
| 1 |
| 4y4 |
分析:根据xy=1,得到y4=
,代入z=
+
,就得到一个关于x和z的式子,把式子的右边化成y=(x-y)2+m的形式,从式子的特点可知当(x-y)2=0时,有最小值m,即可得到答案.
| 1 |
| x4 |
| 1 |
| x4 |
| 1 |
| 4y4 |
解答:解:∵xy=1,
∴x4y4=1,
∴y4=
,
∴z=
+
,
=
+
x4,
=(
-
x2)2+2•
•
x2,
=(
-
x2)2+1,
∵当(
-
x2)2=0,上式有最小值,最小值是1,
即:
-
x2=0,
解得:x=
.
故答案为:
,1.
∴x4y4=1,
∴y4=
| 1 |
| x4 |
∴z=
| 1 |
| x4 |
| 1 |
| 4y4 |
=
| 1 |
| x4 |
| 1 |
| 4 |
=(
| 1 |
| x2 |
| 1 |
| 2 |
| 1 |
| x2 |
| 1 |
| 2 |
=(
| 1 |
| x2 |
| 1 |
| 2 |
∵当(
| 1 |
| x2 |
| 1 |
| 2 |
即:
| 1 |
| x2 |
| 1 |
| 2 |
解得:x=
| 4 | 2 |
故答案为:
| 4 | 2 |
点评:本题主要考查了二次函数的最值,解此题的关键是把关于z的式子化成y=(x-y)2+m的形式.题型较好,但有一定的难度.

练习册系列答案
相关题目
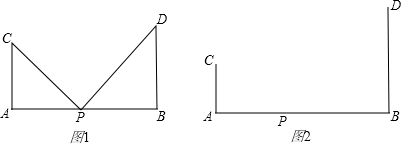

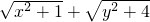 的最小值.分析:(1)如图(1),作长为6的线段AB,过A、B两点在同侧各做AC⊥AB,BD⊥AB,使AC=1,BD=2.
的最小值.分析:(1)如图(1),作长为6的线段AB,过A、B两点在同侧各做AC⊥AB,BD⊥AB,使AC=1,BD=2. ,PD=
,PD=


 +
+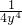 的最小值为________.
的最小值为________. 的最小值.分析:(1)如图(1),作长为6的线段AB,过A、B两点在同侧各做AC⊥AB,BD⊥AB,使AC=1,BD=2.
的最小值.分析:(1)如图(1),作长为6的线段AB,过A、B两点在同侧各做AC⊥AB,BD⊥AB,使AC=1,BD=2. ,PD=
,PD=

 的最小值.问题:①在图(2)中作出符合上述要求的点.
的最小值.问题:①在图(2)中作出符合上述要求的点. 的最小值为______
的最小值为______