题目内容
19、我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图1可以用来解释a2-b2=（a+b）（a-b）．那么通过图2面积的计算，验证了一个恒等式，此等式是（a+b）2-（a-b）2=4ab
．分析：此题根据面积的不同求解方法，可得到不同的表示方法．一种可以是大正方形的面积减去小正方形的面积，还可以表示成4个小长方形的面积；由面积相等，可得等式（a+b）2-（a-b）2=4ab．
解答：解：由图②，可知：
大正方形的面积为：（a+b）2，小正方形的面积为（a-b）2，
∴阴影部分的面积为：（a+b）2-（a-b）2，
∵阴影部分的面积还可表示为：4ab，
∴（a+b）2-（a-b）2=4ab．
大正方形的面积为：（a+b）2，小正方形的面积为（a-b）2，
∴阴影部分的面积为：（a+b）2-（a-b）2，
∵阴影部分的面积还可表示为：4ab，
∴（a+b）2-（a-b）2=4ab．
点评：本题考查了完全平方公式几何意义，解题的关键是注意图形的分割与拼合，会用不同的方法表示同一图形的面积．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
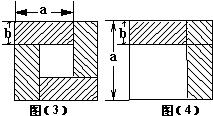6、我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图（3）可以用来解释（a+b）2-（a-b）2=4ab．那么通过图（4）面积的计算，验证了一个恒等式，此等式是（ ）
我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图甲可以用来解释（a+b）2-（a-b）2=4ab．那么通过图乙面积的计算，验证了一个恒等式，此等式是（ ）