题目内容
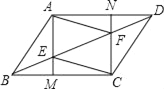
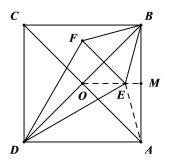
【题目】如图,正方形![]() 的对角线交于点O,
的对角线交于点O,![]() ,
,![]() .
.
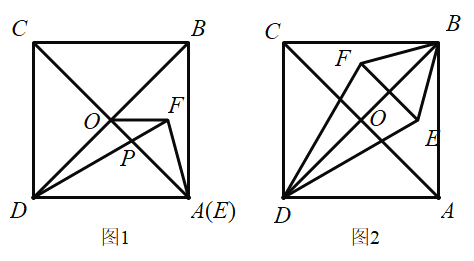
(1)在图1中,点A与点E重合,![]() 与
与![]() 相交于点P,连接
相交于点P,连接![]() ,求证:
,求证:![]() 是等腰三角形.
是等腰三角形.
(2)猜想![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
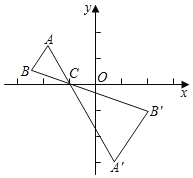
(3)如图2,将![]() 绕点D逆时针旋转
绕点D逆时针旋转![]() 度角(
度角(![]() ).
).
①当旋转角为30°时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
②在旋转的过程中,是否存在![]() 为等腰三角形的情况?如果存在,直接写出旋转的度数;如果不存在,直接作出判断,不必说明理由.
为等腰三角形的情况?如果存在,直接写出旋转的度数;如果不存在,直接作出判断,不必说明理由.
【答案】(1)证明见解析;(2)![]() ,理由见解析;(3)①
,理由见解析;(3)①![]() 是等边三角形,理由见解析;②存在,旋转的角度为
是等边三角形,理由见解析;②存在,旋转的角度为![]() 或
或![]() .
.
【解析】
(1)先根据等腰三角形的性质、三角形的内角和定理可得![]() 和
和![]() 的度数,再根据正方形的性质可得
的度数,再根据正方形的性质可得![]() ,从而可得
,从而可得![]() 的度数,然后根据三角形的内角和定理可得
的度数,然后根据三角形的内角和定理可得![]() 的度数,最后根据等腰三角形的定义即可得证;
的度数,最后根据等腰三角形的定义即可得证;
(2)如图(见解析),过点O作![]() 于点G,过点F作
于点G,过点F作![]() 于点H,先根据正方形的性质得出
于点H,先根据正方形的性质得出![]() ,再根据等腰三角形的三线合一、直角三角形的性质得出
,再根据等腰三角形的三线合一、直角三角形的性质得出![]() ,然后根据直角三角形的性质可得
,然后根据直角三角形的性质可得![]() ,最后根据矩形的判定与性质即可得;
,最后根据矩形的判定与性质即可得;
(3)①先根据旋转的性质得出![]() ,再根据正方形的性质、角的和差得出
,再根据正方形的性质、角的和差得出![]() ,从而可得
,从而可得![]() 垂直平分EF,然后根据垂直平分线的性质可得
垂直平分EF,然后根据垂直平分线的性质可得![]() ,又根据(2)的结论、等腰三角形的三线合一可得
,又根据(2)的结论、等腰三角形的三线合一可得![]() 垂直平分AB,从而可得
垂直平分AB,从而可得![]() ,最后根据等量代换可得
,最后根据等量代换可得![]() ,由此即可得出结论;
,由此即可得出结论;
②根据等腰三角形的定义,分![]() 、
、![]() 和
和![]() ,先确定点E、F的运动轨迹,从而可得
,先确定点E、F的运动轨迹,从而可得![]() 为等腰三角形时,点E、F的位置,再结合①的结论,三角形全等的判定定理与性质求解即可得.
为等腰三角形时,点E、F的位置,再结合①的结论,三角形全等的判定定理与性质求解即可得.
(1)![]() ,点A与点E重合,
,点A与点E重合,![]()
![]() ,
,![]()
![]()
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]()
![]()
![]()
![]()
![]() 是等腰三角形;
是等腰三角形;
(2)![]() ,理由如下:
,理由如下:
如图,过点O作![]() 于点G,过点F作
于点G,过点F作![]() 于点H,则
于点H,则![]()
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]()
![]() 是等腰直角三角形
是等腰直角三角形![]() 斜边上的中线(等腰三角形的三线合一)
斜边上的中线(等腰三角形的三线合一)
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
![]() 四边形OFHG是平行四边形
四边形OFHG是平行四边形
![]()
![]() 平行四边形OFHG是矩形
平行四边形OFHG是矩形
![]() ;
;
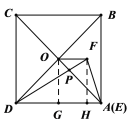
(3)①![]() 是等边三角形,理由如下:
是等边三角形,理由如下:
由旋转的性质得:![]()
![]()
由正方形的性质得:![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,即
,即![]() 平分
平分![]()
![]()
![]() 是等腰三角形
是等腰三角形
![]() 垂直平分EF(等腰三角形的三线合一)
垂直平分EF(等腰三角形的三线合一)
![]()
如图,连接OE、AE,延长OE交AB于点M
由(2)可知,![]()
![]()
![]()
![]() 是等腰三角形
是等腰三角形
![]() 垂直平分AB(等腰三角形的三线合一)
垂直平分AB(等腰三角形的三线合一)
![]()
![]()
![]() 是等边三角形;
是等边三角形;
②根据等腰三角形的定义,分以下三种情况:
(ⅰ)当![]() 时,
时,![]() 为等腰三角形
为等腰三角形
由①可知,此时旋转的度数![]()
(ⅱ)当![]() 时,
时,![]() 为等腰三角形
为等腰三角形
如图,由题意可知,在旋转的过程中,点E、F的运动轨迹在以点D为圆心,DA长为半径的圆上
过点O作![]() 的平行线,交圆D于点P
的平行线,交圆D于点P
由①可知,![]()
由三角形的三边关系定理得:![]()
则以点B为圆心,BP长为半径画圆,与圆D必相交于两点,即点P、Q
即只有当点E运动至点P或点Q时,才有![]()
当点E运动至点P时,由①可知,此时旋转的度数![]()
当点E运动至点Q时,连接BQ、CQ、DQ
则![]()
由①可知,![]() 为等边三角形,
为等边三角形,![]()
![]() ,
,![]()
在![]() 和
和![]() 中,
中,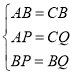
![]()
![]()
![]()
![]()
由旋转的性质知,![]()
![]()
![]()
则此时旋转的角度为![]()
故此时![]() 或
或![]()
(ⅲ)当![]() 时,
时,![]() 为等腰三角形
为等腰三角形
同(ⅱ)可得:此时![]() 或
或![]()
![]()
![]()
综上,在旋转的过程中,存在![]() 为等腰三角形的情况,此时旋转的角度为
为等腰三角形的情况,此时旋转的角度为![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案