ƒøƒ⁄»ð
°æƒø°ø ˝÷·…œ![]() °¢
°¢![]() ∂‘”¶µƒ ˝∑÷±Œ™
∂‘”¶µƒ ˝∑÷±Œ™![]() °¢
°¢![]() £¨«“
£¨«“![]() £¨µ„
£¨µ„![]() « ˝÷·…œ“ª∏ˆ∂ص„£Æ
« ˝÷·…œ“ª∏ˆ∂ص„£Æ
£®![]() £©«Û
£©«Û![]() °¢
°¢![]() µƒ÷µ£¨≤¢‘⁄ ˝÷·…œ±Í≥ˆ
µƒ÷µ£¨≤¢‘⁄ ˝÷·…œ±Í≥ˆ![]() °¢
°¢![]() µƒŒª÷√£Æ
µƒŒª÷√£Æ
£®![]() £© ˝÷·…œ“ªµ„
£© ˝÷·…œ“ªµ„![]() æý¿Î
æý¿Î![]() µ„
µ„![]() ∏ˆµ•Œª≥§∂»£¨∆‰∂‘”¶µƒ ˝
∏ˆµ•Œª≥§∂»£¨∆‰∂‘”¶µƒ ˝![]() ¬˙◊„
¬˙◊„![]() £¨«Ûµ„
£¨«Ûµ„![]() ∂‘”¶µƒ ˝£Æ
∂‘”¶µƒ ˝£Æ
£®![]() £©∂ص„
£©∂ص„![]() ¥”‘≠µ„ø™ ºµ⁄“ª¥ŒœÚ◊Û“∆∂Ø
¥”‘≠µ„ø™ ºµ⁄“ª¥ŒœÚ◊Û“∆∂Ø![]() ∏ˆµ•Œª≥§∂»£¨µ⁄∂˛¥ŒœÚ”““∆∂Ø
∏ˆµ•Œª≥§∂»£¨µ⁄∂˛¥ŒœÚ”““∆∂Ø![]() ∏ˆµ•Œª≥§∂»£¨µ⁄»˝¥ŒœÚ◊Û“∆∂Ø
∏ˆµ•Œª≥§∂»£¨µ⁄»˝¥ŒœÚ◊Û“∆∂Ø![]() ∏ˆµ•Œª≥§∂»£¨µ⁄Àƒ¥ŒœÚ”““∆∂Ø
∏ˆµ•Œª≥§∂»£¨µ⁄Àƒ¥ŒœÚ”““∆∂Ø![]() ∏ˆµ•Œª≥§∂»£¨
∏ˆµ•Œª≥§∂»£¨ ![]() £¨µ„
£¨µ„![]() ƒÐ“∆∂ØµΩ”Î
ƒÐ“∆∂ØµΩ”Î![]() ªÚ’þ
ªÚ’þ![]() ÷ÿ∫œµƒŒª÷√¬£ø»ÙƒÐ£¨ ‘ÃΩÀ˜µ⁄º∏¥Œ“∆∂Ø ±÷ÿ∫œ£ª»Ù≤ªƒÐ£¨«ÎÀµ√˜¿Ì”…£Æ
÷ÿ∫œµƒŒª÷√¬£ø»ÙƒÐ£¨ ‘ÃΩÀ˜µ⁄º∏¥Œ“∆∂Ø ±÷ÿ∫œ£ª»Ù≤ªƒÐ£¨«ÎÀµ√˜¿Ì”…£Æ
£®![]() £©‘⁄£®
£©‘⁄£®![]() £©µƒÃıº˛œ¬£¨«Ûµ„
£©µƒÃıº˛œ¬£¨«Ûµ„![]() “∆∂Ø
“∆∂Ø![]() ¥Œ∫ÛÀ˘±Ì 浃 ˝£Æ
¥Œ∫ÛÀ˘±Ì 浃 ˝£Æ
![]()
°æ¥∞∏°ø£®![]() £©
£©![]() £ª£®
£ª£®![]() £©
£©![]() £ª£®
£ª£®![]() £©¥∞∏º˚Ω‚Œˆ£ª£®
£©¥∞∏º˚Ω‚Œˆ£ª£®![]() £©
£©![]() £Æ
£Æ
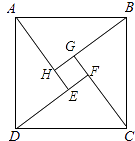
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©∏˘æð∆Ω∑Ω”Îæ¯∂‘÷µµƒ∫ÕŒ™0£¨ø…µ√∆Ω∑Ω”Îæ¯∂‘÷µÕ¨ ±Œ™0£¨ø…µ√a°¢bµƒ÷µ£¨¥”∂¯ø…µ√A,BµƒŒª÷√£ª
£®2£©∏˘æð¡Ωµ„º‰µƒæý¿Îπ´ Ω£¨ø…µ√¥∞∏£ª
£®3£©£®4£©∏˘æðπ€≤Ï£¨ø…∑¢œ÷πʬ…£¨∏˘æðπʬ…£¨ø…µ√¥∞∏£Æ
‘Ã‚Ω‚Œˆ£∫£®![]() £©”…“‚ø…µ√£∫
£©”…“‚ø…µ√£∫  £¨Ω‚µ√£∫
£¨Ω‚µ√£∫ ![]() £Æ
£Æ
![]()
£®2£©°þAC=24£¨µ„A±Ì 浃 ˝Œ™20£¨°ýµ„C±Ì 浃 ˝Œ™44ªÚ-4£Æ
°þ|ac|=-ac£¨°ýa°¢c“Ï∫≈£¨°ýc=-4£Æº¥c∂‘”¶µƒ ˝Œ™-4£Æ
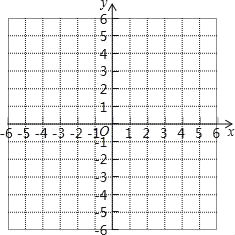
£®![]() £©
£©

P£∫ ![]() £¨
£¨
µ±n=10 ±£¨P=10£Æ
µ±n=20 ±£¨P=20£Æ
°ýµ„Pµ⁄20¥Œ“∆∂ؔε„A÷ÿ∫œ£¨≤ªƒÐ”ε„B÷ÿ∫œ£Æ
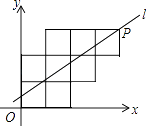
£®4£©»ÙnŒ™∆Ê ˝£¨P=-n£¨»ÙnŒ™≈º ˝£¨P=n£Æ
π P£∫ ![]() £¨
£¨

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏°æƒø°øƒ≥÷–—ß¿∫«Ú∂”12√˚∂”‘±µƒƒÍ¡‰»Á±Ì£∫
ƒÍ¡‰£®ÀÍ£© | 13 | 14 | 15 | 16 |
»À ˝ | 1 | 5 | 4 | 2 |
πÿ”⁄’‚12√˚∂”‘±ƒÍ¡‰µƒƒÍ¡‰£¨œ¬¡–Àµ∑®¥ÌŒÛµƒ «£®°°°°£©
A.÷⁄ ˝ «14
B.º´≤Ó «3
C.÷–Œª ˝ «14.5
D.∆Ωæ˘ ˝ «14.8