Question

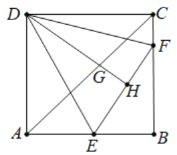
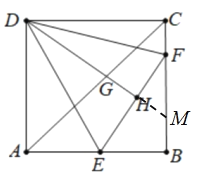
【题目】如图，正方形ABCD的边长为4，将△ADE和△CDF分别沿直线DE和DF折叠后，点A和点C同时落在点H处，且E是AB中点，射线DH交AC于G，交CB于M，则GH的长是__．

Answer 1

【答案】

【解析】

延长DH交BC于M，根据折叠的性质得到DH＝AD＝4，∠DAE＝∠DHE＝∠DCF＝∠DHF＝90°，EH＝AE＝2，CF＝FH，进而可证得点E、H、F在同一直线上，设CF＝FH＝x，则BF＝4﹣x，EF＝2+x，根据勾股定理得到CF＝FH＝，再根据相似三角形的判定和性质定理即可得到答案．

解：延长DH交BC于M，

∵四边形ABCD是正方形，

∴CD＝AD＝BC＝4，∠DAE＝∠BCD＝90°，AD∥BC，

∵E为AB的中点，

∴AE＝BE＝AB＝2，

∵将△ADE和△CDF分别沿直线DE和DF折叠后，点A和点C同时落在点H处，

∴DH＝AD＝4，∠DAE＝∠DHE＝∠DCF＝∠DHF＝90°，EH＝AE＝2，CF＝FH，

∴∠DHE+∠DHF＝180°，

∴点E、H、F在同一直线上，

设CF＝FH＝x，

则BF＝4﹣x，EF＝2+x，

在Rt△BEF中，由勾股定理得：

EF2＝BF2+BE2，

即（2+x）2＝（4﹣x）2+22，

解得：x＝，

∴CF＝FH＝，EF＝，BF＝，

∵∠FHM＝∠B＝90°，∠HFM＝∠BFE，

∴△FHM∽△FBE，

∴，

即，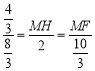

解得：MF＝，MH＝1，

∴DM＝4+1＝5，CM＝+＝3，

∵AD∥BC，

∴△AGD∽△CGM，

∴，

即，

解得：DG＝，

∴GH＝DH﹣DG＝4﹣＝，

故答案为：．