题目内容
【题目】已知抛物线y=﹣
x2+bx+c经过点（1，0），（0，
）．
（1）求该抛物线的函数表达式；
（2）将抛物线y=﹣x2+bx+c平移，使其顶点恰好落在原点，请写出一种平移的方法及平移后的函数表达式．
【答案】（1）抛物线解析式为y=﹣
x2﹣x+
；（2）抛物线向右平移一个单位，向下平移2个单位，解析式变为y=﹣x2
【解析】
(1)将(1,0)和(0,号)代入抛物线解析式得到-个关于b和c的二元-次方程组,解之即可得抛物线解析式.
(2)将(1)中求得的解析式配方得其顶点坐标为(-1,2),故使其顶点恰好落在原点的一种平移方法:先向右平移1个单位长度,再向下平移2个单位长度;从而可得平移后的函数表达式.
（1）把（1，0），（0，
）代入抛物线解析式得：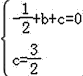
，
解得：
，
则抛物线解析式为y=﹣x2﹣x+；
（2）抛物线解析式为y=﹣
x2﹣x+
=﹣（x+1）2+2，
将抛物线向右平移一个单位，向下平移2个单位，解析式变为y=﹣x2．
练习册系列答案
相关题目
【题目】甲、乙两名队员参加射击训练，每人射击10次，成绩分别如下：
根据以上信息，整理分析数据如下：
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
（1）a＝_____；b＝_____；c＝_____；
（2）填空：（填“甲”或“乙”）．
①从平均数和中位数的角度来比较，成绩较好的是_____；
②从平均数和众数的角度来比较，成绩较好的是_____；
③成绩相对较稳定的是_____．
