题目内容
已知二次函数y=x2+2ax+b的图象与x轴的两个交点的横坐标x1，x2满足：1≤x1＜x2≤2．
证明：（Ⅰ）b＜a2；（Ⅱ）0＜a+b＜2．
证明：（Ⅰ）∵与x轴有两个交点，
∴△=b2-4ac=（2a）2-4×1×b＞0，
整理得，b＜a2；
（Ⅱ）根据根与系数的关系，x1+x2=-
=-
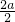=-a，
x1•x2=
=
=b，
∵1≤x1＜x2≤2，
∴2＜-a＜4，1＜b＜4，
∴-4＜a＜-2，
∴-3＜a+b＜2，
又∵1≤x1＜x2≤2，
∴a、b都是正数，
∴0＜a+b＜2．
分析：（Ⅰ）利用根的判别式列式整理即可得解；
（Ⅱ）利用根与系数的关系列式表示出a、b的取值范围，再根据a、b都是正数即可证明．
点评：本题考查了抛物线与x轴的交点问题，根的判别式与根与系数的关系，需要注意根据两个根都是正数的条件可知a、b都是正数的利用．
∴△=b2-4ac=（2a）2-4×1×b＞0，
整理得，b＜a2；
（Ⅱ）根据根与系数的关系，x1+x2=-
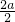=-=-a，x1•x2=
==b，∵1≤x1＜x2≤2，
∴2＜-a＜4，1＜b＜4，
∴-4＜a＜-2，
∴-3＜a+b＜2，
又∵1≤x1＜x2≤2，
∴a、b都是正数，
∴0＜a+b＜2．
分析：（Ⅰ）利用根的判别式列式整理即可得解；
（Ⅱ）利用根与系数的关系列式表示出a、b的取值范围，再根据a、b都是正数即可证明．
点评：本题考查了抛物线与x轴的交点问题，根的判别式与根与系数的关系，需要注意根据两个根都是正数的条件可知a、b都是正数的利用．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．