题目内容
在△ABC中,
(1)如图一,AB、AC边上的高CE、BD交于点O,若∠A=60°,则∠BOC=
(2)如图二,若∠A为钝角,请画出AB、AC边上的高CE、BD,CE、BD所在直线交于点O,则∠BAC+∠BOC=
(3)由(1)(2)可以得到,无论∠A为锐角还是钝角,总有∠BAC+∠BOC=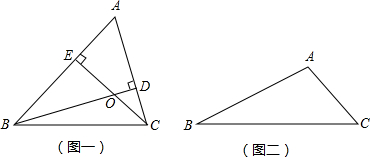
(1)如图一,AB、AC边上的高CE、BD交于点O,若∠A=60°,则∠BOC=
120
120
°.(2)如图二,若∠A为钝角,请画出AB、AC边上的高CE、BD,CE、BD所在直线交于点O,则∠BAC+∠BOC=
180
180
°,再用你已学过的数学知识加以说明.(3)由(1)(2)可以得到,无论∠A为锐角还是钝角,总有∠BAC+∠BOC=
180
180
°.
分析:(1)根据直角三角形两锐角互余求出∠ABD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可求出∠BOC;
(2)设∠BAC=x,根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ABD,再根据直角三角形两锐角互余表示出∠BOC,二者相加即可得解;
(3)根据计算即可得出规律.
(2)设∠BAC=x,根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ABD,再根据直角三角形两锐角互余表示出∠BOC,二者相加即可得解;
(3)根据计算即可得出规律.
解答: 解:(1)∵∠A=60°,BD是AC边上的高,
解:(1)∵∠A=60°,BD是AC边上的高,
∴∠ABD=90°-∠A=90°-60°=30°,
∵CE是AB边上的高,
∴在Rt△BOE中,∠BOC=∠ABD+∠BEO=30°+90°=120°;
(2)如图所示,设∠BAC=x,
∵BD是AC边上的高,
∴∠ABD=∠BAC-∠ADB=x-90°,
∵CE是AB边上的高,
∴∠BOC=90°-∠ABD=90°-(x-90°)=180°-x,
∴∠BAC+∠BOC=x+180°-x=180°;
(3)根据计算,无论∠A为锐角还是钝角,总有∠BAC+∠BOC=180°.
故答案为:(1)120;(2)180;(3)180.
 解:(1)∵∠A=60°,BD是AC边上的高,
解:(1)∵∠A=60°,BD是AC边上的高,∴∠ABD=90°-∠A=90°-60°=30°,
∵CE是AB边上的高,
∴在Rt△BOE中,∠BOC=∠ABD+∠BEO=30°+90°=120°;
(2)如图所示,设∠BAC=x,
∵BD是AC边上的高,
∴∠ABD=∠BAC-∠ADB=x-90°,
∵CE是AB边上的高,
∴∠BOC=90°-∠ABD=90°-(x-90°)=180°-x,
∴∠BAC+∠BOC=x+180°-x=180°;
(3)根据计算,无论∠A为锐角还是钝角,总有∠BAC+∠BOC=180°.
故答案为:(1)120;(2)180;(3)180.
点评:本题考查了三角形的内角和定理,三角形的高线以及三角形的一个外角等于与它不相邻的两个内角的和的性质,是基础题,熟记定理与性质并准确识图找准各角度之间的关系是解题的关键.

练习册系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于