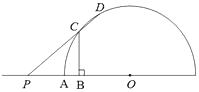
题目内容
【题目】如图1,在 ![]() 中,以
中,以 ![]() 为直径的⊙O,交
为直径的⊙O,交 ![]() 于点
于点 ![]() ,且
,且 ![]() ,交线段
,交线段 ![]() 的延长线于点
的延长线于点 ![]() ,连接
,连接 ![]() ,过点
,过点 ![]() 作
作 ![]() 于点
于点 ![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)在 ![]() 的内部作
的内部作 ![]() ,使
,使 ![]() ,
, ![]() 分别交于
分别交于 ![]() 、
、 ![]() 于点
于点 ![]() 、
、 ![]() ,交⊙O于点
,交⊙O于点 ![]() ,若
,若 ![]() ,求
,求 ![]() 的长.
的长.
【答案】(Ⅰ)证明:过点C作CH⊥BA 交BA的延长线于H,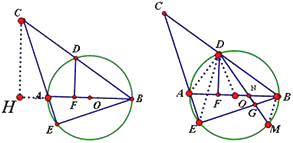
∵ ![]() ,
, ![]() ,
,
∴DF为![]() BHC的中位线,CH=2DF,
BHC的中位线,CH=2DF,
连接AD,
∵AB是直径,
∴∠ADB=90°,
又∵BD=CD,
∴![]() ABC是等腰三角形∴AB=AC,
ABC是等腰三角形∴AB=AC,
∵∠AEB =90°=∠AHC ,∠BAE =∠CAH
∴![]() AEB≌
AEB≌![]() AHC
AHC
∴CH=BE , ![]()
(Ⅱ)解:连接DA、DO、DE、BM,
∴∠ADE=∠ABE=∠BDM
∵ ![]() , BN=
, BN= ![]() ,
,
∴由(Ⅰ)可知, BE=2DF= ![]() ,
,
∵⊿CEB为直角三角形, BD=CD,
∴DE=DB , 又∠ADE=∠BDN ∠AED=∠DBN
∴![]() ADE≌
ADE≌![]() NDB
NDB
∴AD=DN BN=AE= ![]()
∵AB是直径,
∴∠ADB=∠AEB =90° BE=2DF= ![]() , AE=
, AE= ![]() . AB=3
. AB=3 ![]()
∵ ![]() AD=DN ∴ FN=AF=
AD=DN ∴ FN=AF= ![]() . DF=
. DF= ![]() ∴DN=3
∴DN=3 ![]()
在![]() ADN与
ADN与![]() BMN中,可证
BMN中,可证![]() ADN∽
ADN∽![]() MBN,得出AN
MBN,得出AN![]() NB=MN
NB=MN![]() DN
DN
∴MN=2 ![]()
在![]() DBG与
DBG与![]() DMB中,
DMB中,
∵DC=DE=DB
∴∠DMB=∠DBE=∠DEB, ∠BDG=∠BDM,
可证![]() DBG∽
DBG∽![]() DMB,
DMB,
得出DB2=DG×DM ![]() ,FB=2
,FB=2 ![]()
∴DB=6, DM=DN+MN=3 ![]() +2
+2 ![]() =5
=5 ![]()
∴36=DG×5 ![]() , DG=
, DG= ![]() ,
,
∴ MG= ![]() .
.
【解析】本题考查全等三角形的判定与性质、相似三角形的判定与性质,注意分析题目中条件,找足![]() AEB和
AEB和![]() AHC全等、
AHC全等、![]() ADE和
ADE和![]() NDB全等,和
NDB全等,和![]() ADN∽
ADN∽![]() MBN、
MBN、![]() DBG∽
DBG∽![]() DMB的条件,推导求解.
DMB的条件,推导求解.
【考点精析】掌握三角形中位线定理和相似三角形的判定与性质是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案