题目内容
已知点A(0,2)、B( ,2)、C(0,4).
,2)、C(0,4).
(1)如图1,连接BO、BC、AB .
①填空:AC的长为 ,AB的长为 ;
②试判断 的形状,并说明理由;
的形状,并说明理由;
(2)如图2,过点C向右作平行于x轴的射线,点P是射线上的动点,连接BP,以BP为一边在△ABP外侧作等边△BPQ,当四边形ABQP为梯形时,求点P的横坐标.
(1)①2,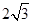 ;②等边三角形;(2)
;②等边三角形;(2)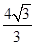 或0或
或0或 .
.
解析试题分析:(1)①根据等边三角形的性质结合点A、B、C的坐标即可求得结果;
②由A(0,2),B(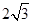 ,2)可得
,2)可得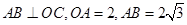 ,在
,在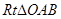 中,根据∠AOB的正切函数值即可得到
中,根据∠AOB的正切函数值即可得到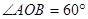 ,同理
,同理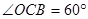 ,即可得到结果;
,即可得到结果;
(2)分三种情况:①当PQ∥AB时,②当P点与C点重合时,③当BP⊥CP时,根据等边三角形的性质、锐角三角函数的定义、梯形的性质分析即可.
(1)①AC的长为2,AB的长为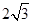 ;
;
②△OBC是等边三角形. 理由如下:
∵A(0,2),B(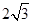 ,2)
,2)
∴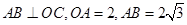
在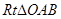 中,
中,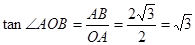
∴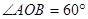 ,同理
,同理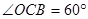
∴△OBC是等边三角形;
(2)分三种情况讨论:
①当PQ∥AB时(如图1):
点Q在CP上,作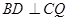 于D,则四边形
于D,则四边形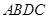 是矩形
是矩形
∴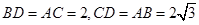
∵△BPQ是等边三角形,
∴BD平分PQ,平分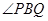
∴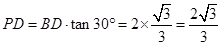
∴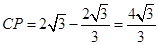
∴点P的横坐标是 ;
;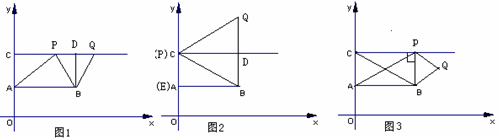
②如图2,当P点与C点重合时,
∵在 中,
中,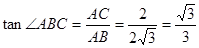
∴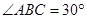 ,∵
,∵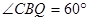
∴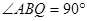 ,∴BQ∥AC,又CQ与AB不平行
,∴BQ∥AC,又CQ与AB不平行
∴四边形 ABQP是梯形.
∴点P的横坐标是0;
③如图3,当BP⊥CP时,
∵CP∥AB
∴BP⊥AB
∵在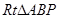 中,
中,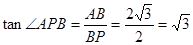
∴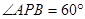
∵△BPQ是等边三角形
∴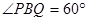
∴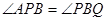
∴AP∥BQ
∴四边形 ABQP是梯形
∴点P的横坐标为
综上所述,四边形ABQP为梯形时,点P的横坐标是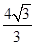 或0或
或0或 .
.
考点:动点的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
 14、如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO=
14、如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO= 2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.