题目内容
如图,已知在□ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:四边形GEHF是平行四边形.

见解析
【解析】
试题分析:根据ABCD为平行四边形得到AB=CD,AB∥CD,根据AG=CH得到BG=DH,从而说明△BEG≌△DFH,所以GE=HF,∠BEG=∠DFH,所以GE∥HF,根据一组对边平行且相等的四边形为平行四边形进行判定.
试题解析:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD∴∠GBE=∠HDF 又∵AG=CH ∴BG=DH
又∵BE=DF ∴△GBE≌△HDF
∴GE=HF, ∠GEB=∠HFD ∴∠GEF=∠HFE ∴GE∥HF
∴四边形GEHF是平行四边形.
考点:平行四边形的判定

练习册系列答案
相关题目
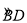 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.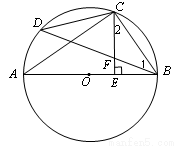


 B.
B. C.
C. D.
D.

 向下平移1个单位,得到的抛物线是 。
向下平移1个单位,得到的抛物线是 。 其中
其中