题目内容
 如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.
如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)菜园的面积能否达到120m2?说明理由.
解:(1)依题意得,矩形的另一边长为 m,
m,
则y=x× =-
=- x2+15x,
x2+15x,
由图形可得,自变量x的取值范围是0<x≤18.
(2)解法一:若能达到,则令y=120,得 ,
,
即x2-30x+240=0,
△b2-4ac=302-4×240<0,该方程无实数根,
所以菜园的面积不能达到120 m2.
解法二:y=- x2+15x=-
x2+15x=- (x-15)2+
(x-15)2+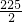 ,
,
当x=15时,y有最大值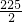 ,
,
即菜园的最大面积为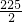 m2,所以菜园的面积不能达到120 m2.
m2,所以菜园的面积不能达到120 m2.
分析:(1)求出矩形的另一边长,根据矩形的面积=长×宽,可得出y与x的函数关系式,结合墙的长度可得出自变量的取值范围;
(2)令y=120,解方程后即可作出判断,也可求出y的最大值,然后与120比较;
点评:本题考查了二次函数的应用及一元二次方程的应用,解答本题的关键是表示出矩形的另一边长,得出y与x的函数关系式,难度一般.
 m,
m,则y=x×
 =-
=- x2+15x,
x2+15x,由图形可得,自变量x的取值范围是0<x≤18.
(2)解法一:若能达到,则令y=120,得
 ,
,即x2-30x+240=0,
△b2-4ac=302-4×240<0,该方程无实数根,
所以菜园的面积不能达到120 m2.
解法二:y=-
 x2+15x=-
x2+15x=- (x-15)2+
(x-15)2+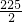 ,
,当x=15时,y有最大值
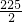 ,
,即菜园的最大面积为
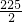 m2,所以菜园的面积不能达到120 m2.
m2,所以菜园的面积不能达到120 m2.分析:(1)求出矩形的另一边长,根据矩形的面积=长×宽,可得出y与x的函数关系式,结合墙的长度可得出自变量的取值范围;
(2)令y=120,解方程后即可作出判断,也可求出y的最大值,然后与120比较;
点评:本题考查了二次函数的应用及一元二次方程的应用,解答本题的关键是表示出矩形的另一边长,得出y与x的函数关系式,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 园的面积y(米2)与x(米)的关系式为
园的面积y(米2)与x(米)的关系式为

