题目内容
 直线
直线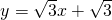 交x轴于A,交y轴于B,将这条直线绕某点顺时针旋转90°且M、N分别为A、B的对应点(M、N在第一象限),直线MN交y轴于C,且S△BCM=S△BMN,双曲线
交x轴于A,交y轴于B,将这条直线绕某点顺时针旋转90°且M、N分别为A、B的对应点(M、N在第一象限),直线MN交y轴于C,且S△BCM=S△BMN,双曲线 过M、N两点,则k=________.
过M、N两点,则k=________.
2
分析:过M、N点分别作x轴、y轴的垂线垂足分别为E、H、F、Q,ME与NQ交与T点,两垂线的交点为P,直线AB绕某点顺时针旋转90°交x轴于K点,先求出A(-1,0),B(0, ),利用勾股定理得到AB=2,则∠OAB=60°,∠OBA=30°,而∠KPA=90°,可得到∠MNT=30°,再利用旋转的性质得到MN=AB=2,则MT=1,NT=
),利用勾股定理得到AB=2,则∠OAB=60°,∠OBA=30°,而∠KPA=90°,可得到∠MNT=30°,再利用旋转的性质得到MN=AB=2,则MT=1,NT= ,设M点坐标为(a,b),则N点坐标为(a+
,设M点坐标为(a,b),则N点坐标为(a+ ,b-1),根据反比例函数图象上点的坐标特点得到k=ab=(a+
,b-1),根据反比例函数图象上点的坐标特点得到k=ab=(a+ )(b-1),即a-
)(b-1),即a- b+
b+ =0①,又S△BCM=S△BMN,则CM=MN,
=0①,又S△BCM=S△BMN,则CM=MN,
得到MH为△CQN的中位线,所以MH= NQ,即a=
NQ,即a= (a+
(a+ ),解得a=
),解得a= ,易求得b=2,于是k=ab=2
,易求得b=2,于是k=ab=2 .
.
解答:过M、N点分别作x轴、y轴的垂线, 垂足分别为E、H、F、Q,ME与NQ交与T点,两垂线的交点为P,直线AB绕某点顺时针旋转90°交x轴于K点,如图所示
垂足分别为E、H、F、Q,ME与NQ交与T点,两垂线的交点为P,直线AB绕某点顺时针旋转90°交x轴于K点,如图所示
对于y= x+
x+ ,令x=0,则y=
,令x=0,则y= ;令y=0,则
;令y=0,则 x+
x+ =0,解得x=1,即A(-1,0),B(0,
=0,解得x=1,即A(-1,0),B(0, ),AB=
),AB= =2,
=2,
则∠OAB=60°,∠OBA=30°,
∵∠KPA=90°,
∴∠PKA=30°,
∴∠MNT=30°,
∵直线AB绕某点顺时针旋转90°且M、N分别为A、B的对应点,
∴MN=AB=2,
∴MT=OA=1,NT=OB= ,
,
设M点坐标为(a,b),则N点坐标为(a+ ,b-1),
,b-1),
∵双曲线 过M、N两点,
过M、N两点,
∴k=ab=(a+ )(b-1),即a-
)(b-1),即a- b+
b+ =0①,
=0①,
∵S△BCM=S△BMN,
∴CM=MN,
∴MH= NQ,即a=
NQ,即a= (a+
(a+ ),解得a=
),解得a= ,
,
把a= 代入①得
代入①得 -
- b+
b+ =0,
=0,
∴b=2,
∴k=ab=2 .
.
故答案为2 .
.
点评:本题考查了反比例函数的综合题:反比例函数图象上点的横纵坐标的积为定值;旋转的性质要熟练运用;勾股定理和含30°的直角三角形三边的关系在几何计算中常用到.

分析:过M、N点分别作x轴、y轴的垂线垂足分别为E、H、F、Q,ME与NQ交与T点,两垂线的交点为P,直线AB绕某点顺时针旋转90°交x轴于K点,先求出A(-1,0),B(0,
 ),利用勾股定理得到AB=2,则∠OAB=60°,∠OBA=30°,而∠KPA=90°,可得到∠MNT=30°,再利用旋转的性质得到MN=AB=2,则MT=1,NT=
),利用勾股定理得到AB=2,则∠OAB=60°,∠OBA=30°,而∠KPA=90°,可得到∠MNT=30°,再利用旋转的性质得到MN=AB=2,则MT=1,NT= ,设M点坐标为(a,b),则N点坐标为(a+
,设M点坐标为(a,b),则N点坐标为(a+ ,b-1),根据反比例函数图象上点的坐标特点得到k=ab=(a+
,b-1),根据反比例函数图象上点的坐标特点得到k=ab=(a+ )(b-1),即a-
)(b-1),即a- b+
b+ =0①,又S△BCM=S△BMN,则CM=MN,
=0①,又S△BCM=S△BMN,则CM=MN,得到MH为△CQN的中位线,所以MH=
 NQ,即a=
NQ,即a= (a+
(a+ ),解得a=
),解得a= ,易求得b=2,于是k=ab=2
,易求得b=2,于是k=ab=2 .
.解答:过M、N点分别作x轴、y轴的垂线,
 垂足分别为E、H、F、Q,ME与NQ交与T点,两垂线的交点为P,直线AB绕某点顺时针旋转90°交x轴于K点,如图所示
垂足分别为E、H、F、Q,ME与NQ交与T点,两垂线的交点为P,直线AB绕某点顺时针旋转90°交x轴于K点,如图所示对于y=
 x+
x+ ,令x=0,则y=
,令x=0,则y= ;令y=0,则
;令y=0,则 x+
x+ =0,解得x=1,即A(-1,0),B(0,
=0,解得x=1,即A(-1,0),B(0, ),AB=
),AB= =2,
=2,则∠OAB=60°,∠OBA=30°,
∵∠KPA=90°,
∴∠PKA=30°,
∴∠MNT=30°,
∵直线AB绕某点顺时针旋转90°且M、N分别为A、B的对应点,
∴MN=AB=2,
∴MT=OA=1,NT=OB=
 ,
,设M点坐标为(a,b),则N点坐标为(a+
 ,b-1),
,b-1),∵双曲线
 过M、N两点,
过M、N两点,∴k=ab=(a+
 )(b-1),即a-
)(b-1),即a- b+
b+ =0①,
=0①,∵S△BCM=S△BMN,
∴CM=MN,
∴MH=
 NQ,即a=
NQ,即a= (a+
(a+ ),解得a=
),解得a= ,
,把a=
 代入①得
代入①得 -
- b+
b+ =0,
=0,∴b=2,
∴k=ab=2
 .
.故答案为2
 .
.点评:本题考查了反比例函数的综合题:反比例函数图象上点的横纵坐标的积为定值;旋转的性质要熟练运用;勾股定理和含30°的直角三角形三边的关系在几何计算中常用到.

练习册系列答案
相关题目
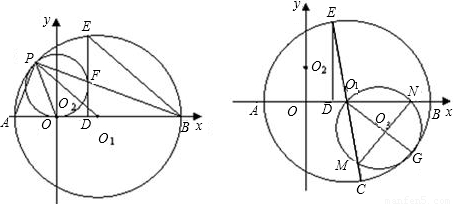
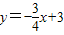 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.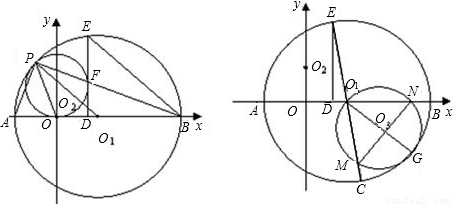
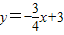 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.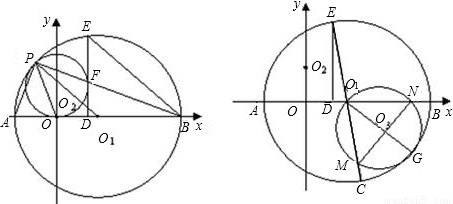
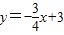 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.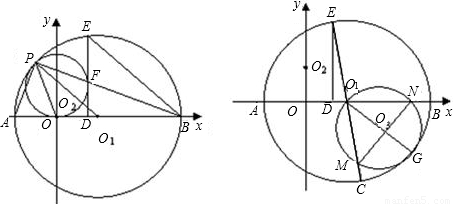
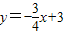 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.