题目内容
☉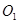 和☉
和☉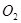 的半径是方程
的半径是方程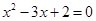 的两根,圆心距
的两根,圆心距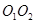 =4,则☉
=4,则☉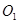 和☉
和☉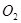 的位置关系是
的位置关系是
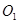 和☉
和☉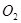 的半径是方程
的半径是方程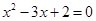 的两根,圆心距
的两根,圆心距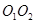 =4,则☉
=4,则☉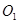 和☉
和☉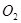 的位置关系是
的位置关系是| A.相离 | B.外离 | C.相交 | D.内含 |
B
试题分析:先由方程
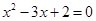 求出方程的两根分别为
求出方程的两根分别为 ,
, ,而圆心距为4, 所以
,而圆心距为4, 所以 ,即两圆外离
,即两圆外离点评:两圆之间有3大关系,即相离、相交、相切,而相离可分为外离和内含,相切可分为内切和外切。若
 ,则两圆外离,若
,则两圆外离,若 ,则两圆内含,若
,则两圆内含,若 ,则两圆外切,若
,则两圆外切,若 ,则两圆内切,若
,则两圆内切,若 ,则两圆相交
,则两圆相交
练习册系列答案
相关题目
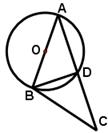
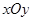 中,原点O是正三角形ABC外接圆的圆心,点A在
中,原点O是正三角形ABC外接圆的圆心,点A在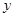 轴的正半轴上,△ABC的边长为6.以原点O为旋转中心将△ABC沿逆时针方向旋转角,得到△
轴的正半轴上,△ABC的边长为6.以原点O为旋转中心将△ABC沿逆时针方向旋转角,得到△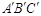 ,点
,点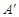 、
、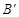 、
、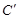 分别为点A、B、C的对应点.
分别为点A、B、C的对应点.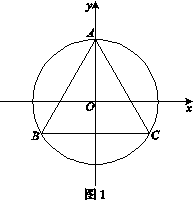
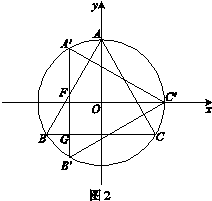
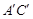 、
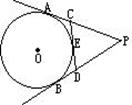
、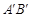 交于点D、E,则DE的长为_______;
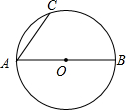
交于点D、E,则DE的长为_______;  ,AB=8,则⊙O的直径为 。
,AB=8,则⊙O的直径为 。
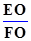 的值.
的值.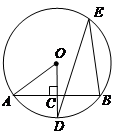
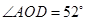 ,求
,求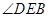 的度数;
的度数;
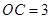 ,
,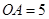 ,求
,求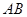 的长.
的长.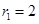 、
、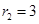 ,若两圆外切,则圆心距O1O2是( )
,若两圆外切,则圆心距O1O2是( )


