题目内容
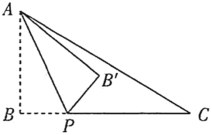
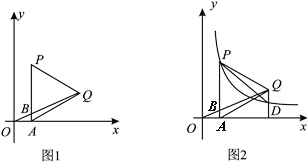
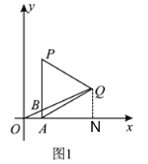
【题目】如图1,P是平面直角坐标系中第一象限内一点,过点P作PA⊥x轴于点A,以AP为边在右侧作等边△APQ,已知点Q的纵坐标为2,连结OQ交AP于B,BQ=3OB.
(1)求点P的坐标;
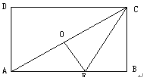
(2)如图2,若过点P的双曲线![]() (k>0)与过点Q垂直于x轴的直线交于D,连接PD.求
(k>0)与过点Q垂直于x轴的直线交于D,连接PD.求![]() .
.
【答案】(1)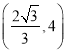 ;(2)
;(2)![]()
【解析】
(1)过点Q作x轴的垂线N,根据△APQ是等边三角形及PA⊥x轴得出∠QAN=90°-60°=30°,因为点Q的纵坐标是2,根据解直角三角形可求出AQ与AN的值,根据△AOB∽△ONQ和BQ=3OB可得OA的值,继而可得点P坐标;
(2)设DQ的延长线与过点P平行于x轴的直线交于点E,将P(![]() ,4)代入
,4)代入![]() 可得双曲线解析式,由(1)得D点横坐标,代入解析式即可求出D的纵坐标,即DN的长,从而得到DE的长,在Rt△PED中,PE=AN,
可得双曲线解析式,由(1)得D点横坐标,代入解析式即可求出D的纵坐标,即DN的长,从而得到DE的长,在Rt△PED中,PE=AN,![]() =
=![]() ,将值代入即可求解.
,将值代入即可求解.
解:(1)过点Q作x轴的垂线N
∵△APQ是等边三角形
∴∠PAQ=60°
∵PA⊥x轴
∴∠QAN=90°-60°=30°
∵点Q的纵坐标是2
∴QN=2
∴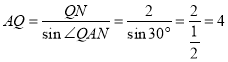
AN=![]() =
=![]() =
=![]()
∴点P纵坐标为4
∵PA⊥x轴,QN⊥x轴
∴△AOB∽△ONQ
∴![]()
∵BQ=3OB
∴![]() =
=![]() =3
=3
∴OA=![]()
∴P点坐标为(![]() ,4).
,4).
故答案为(![]() ,4).
,4).
(2)设DQ的延长线与过点P平行于x轴的直线交于点E

将P(![]() ,4)代入
,4)代入![]() ,得
,得
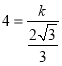
解得k=![]()
∴双曲线解析式为![]()
由(1)知N点横坐标为![]() +
+![]() =
=![]()
即D点横坐标为![]()
∴D点纵坐标为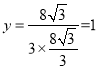
∴DN=1
∴DQ=QN-DN=2-1=1
∴DE=4-1=3
在Rt△PED中,PE=AN=![]()
∴![]() =
=![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目