题目内容
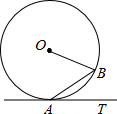如图，AT是⊙O的切线，AB是⊙O的弦，∠B=55°，则∠BAT等于
- A.45°
- B.40°
- C.35°
- D.30°
C
分析：连接OA，则∠AOB=2∠BAT，∠OAT=90°，故可用∠BAT表示出∠OAB的度数，再根据三角形的内角和定理解答即可．
解答：
解：连接OA，则∠AOB=2∠BAT，OA⊥AT，
∵OA⊥AT，
∴∠OAT=90°，
∴∠OAB=90°-∠BAT，
∵∠B+∠AOB+∠OAB=180°，
∴∠B+2∠BAT+90°-∠BAT=180°，
解得∠BAT=35°．
故选C．
点评：本题考查的是切线的性质及三角形内角和定理，解答此类问题往往通过作辅助线连接圆心和切点，利用垂直关系求解．
分析：连接OA，则∠AOB=2∠BAT，∠OAT=90°，故可用∠BAT表示出∠OAB的度数，再根据三角形的内角和定理解答即可．
解答：
解：连接OA，则∠AOB=2∠BAT，OA⊥AT，∵OA⊥AT，
∴∠OAT=90°，
∴∠OAB=90°-∠BAT，
∵∠B+∠AOB+∠OAB=180°，
∴∠B+2∠BAT+90°-∠BAT=180°，
解得∠BAT=35°．
故选C．
点评：本题考查的是切线的性质及三角形内角和定理，解答此类问题往往通过作辅助线连接圆心和切点，利用垂直关系求解．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
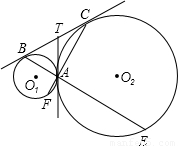
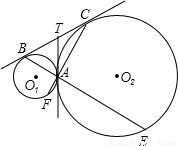
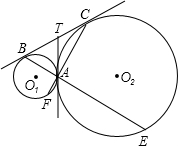切线，AT与BC相交于点T．延长BA、CA，分别与两圆交于点E、F．
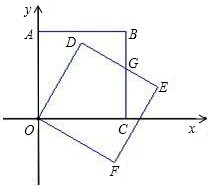在直角坐标系中，正方形OABC的两边OC、OA分别在x轴、y轴上，A点的坐标为（0、4）．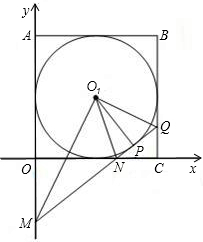
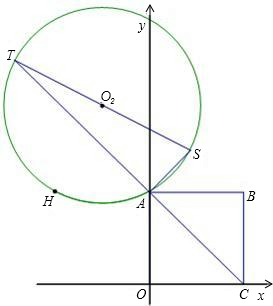
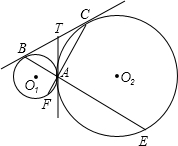切线，AT与BC相交于点T．延长BA、CA，分别与两圆交于点E、F．
