��Ŀ����
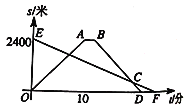
����Ŀ��С�����ù��������Ӽҳ������������е����![]() ��ͼ��ݻ��飮С��������ͬʱ�����İְ���ÿ����
��ͼ��ݻ��飮С��������ͬʱ�����İְ���ÿ����![]() ���ٶȴ�ͼ�����ͬһ����·���лؼң�С����ͼ���ͣ����
���ٶȴ�ͼ�����ͬһ����·���лؼң�С����ͼ���ͣ����![]() ���Ӻ���ԭ·��ԭ�ٷ��أ������dz�����
���Ӻ���ԭ·��ԭ�ٷ��أ������dz�����![]() ���֣�ʱ��С�����֮��ľ���Ϊ
���֣�ʱ��С�����֮��ľ���Ϊ![]() ���ף���С���ְ����֮��ľ���Ϊ
���ף���С���ְ����֮��ľ���Ϊ![]() ���ף���ͼ������
���ף���ͼ������![]() ���߶�
���߶�![]() �ֱ��ʾ
�ֱ��ʾ![]() ��
��![]() ��
��![]() ֮��ĺ�����ϵ��ͼ��С���Ӽҳ���������___�����ڷ���;���ϰְ֣�
֮��ĺ�����ϵ��ͼ��С���Ӽҳ���������___�����ڷ���;���ϰְ֣�
���𰸡�̽��һ����FDC+��ECD=180��+��A��̽��������DPC=90��+![]() ��A��̽��������DPC=
��A��̽��������DPC=![]() ����A+��B����̽���ģ���P=
����A+��B����̽���ģ���P=![]() ����A+��B+��E+��F��-180��.
����A+��B+��E+��F��-180��.
��������
̽��һ�����������ε�һ����ǵ������������ڵ������ڽǵĺͿɵá�FDC=��A+��ACD����ECD=��A+��ADC���ٸ����������ڽǺͶ����������ɵý⣻
̽���������ݽ�ƽ���ߵĶ���ɵá�PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��ACD��Ȼ������������ڽǺͶ�����ʽ�������ɵý⣻
��ACD��Ȼ������������ڽǺͶ�����ʽ�������ɵý⣻
̽�����������ı��ε��ڽǺͶ�����ʾ����ADC+��BCD��Ȼ��ͬ��̽������ɣ�
̽���ģ����������ε��ڽǺ�ʽ��ʾ����EDC+��BCD��Ȼ��ͬ��̽������ɣ�
�⣺̽��һ���ߡ�FDC=��A+��ACD����ECD=��A+��ADC��
���FDC+��ECD=��A+��ACD+��A+��ADC=180��+��A��
̽��������DP��CP�ֱ�ƽ�֡�ADC�͡�ACD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��ACD��
��ACD��
���DPC=180��-��PDC-��PCD��
=180��-![]() ��ADC-
��ADC-![]() ��ACD��
��ACD��
=180��-![]() ����ADC+��ACD����
����ADC+��ACD����
=180��-![]() ��180��-��A����
��180��-��A����
=90��+![]() ��A��
��A��
̽��������DP��CP�ֱ�ƽ�֡�ADC�͡�BCD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��BCD��
��BCD��
���DPC=180��-��PDC-��PCD��
=180��-![]() ��ADC-
��ADC-![]() ��BCD��
��BCD��
=180��-![]() ����ADC+��BCD����
����ADC+��BCD����
=180��-![]() ��360��-��A-��B����
��360��-��A-��B����
=![]() ����A+��B����
����A+��B����
̽���ģ�������ABCDEF���ڽǺ�Ϊ����6-2��180��=720����
��DP��CP�ֱ�ƽ�֡�EDC�͡�BCD��
���PDC=![]() ��EDC����PCD=
��EDC����PCD=![]() ��BCD��
��BCD��
���P=180��-��PDC-��PCD
=180��-![]() ��EDC-
��EDC-![]() ��BCD
��BCD
=180��-![]() ����EDC+��BCD��
����EDC+��BCD��
=180��-![]() ��720��-��A-��B-��E-��F��
��720��-��A-��B-��E-��F��
=![]() ����A+��B+��E+��F��-180����
����A+��B+��E+��F��-180����
����P=![]() ����A+��B+��E+��F��-180����
����A+��B+��E+��F��-180����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�