Question

【题目】如图已知，于点，于点交于点．，，．

（1）若，点是上一点，当点到点和点的距离相等时，求的长；

（2）若，点是上一点，点是上一点，连接，，，求的最小值．

Answer 1

【答案】（1） （2）

【解析】

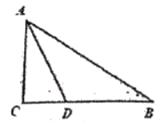
（1）如图1中，连接AB，作线段AB的中垂线MN，交AB于N，交EF于M，连接AM，BM．设DM=x．根据MA=MB构建方程即可解决问题；
（2）如图2中，如图，作点A故直线GH 的对称点A′，点B关于直线EF的对称点B′，连接A′B′交GH于点P，交EF于点Q，作B′H⊥CA交CA的延长线于H．则此时AP+PQ+QB的值最小．最小值为线段A′B′的长；

解：（1）如图1中，连接AB，作线段AB的中垂线MN，交AB于N，交EF于M，连接AM，BM．设DM=x．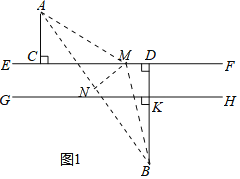

在Rt△ACM中，AM2=AC2+CM2=32+（6-x）2，
在Rt△BDM中，BM2=DM2+BD2=x2+62，
∵AM=MB，
∴32+（6-x）2=x2+62，
解得x=，
∴CM=CD-MD=6- = ．
（2）如图2中，如图，作点A故直线GH 的对称点A′，点B关于直线EF的对称点B′，连接A′B′交GH于点P，交EF于点Q，作B′H⊥CA交CA的延长线于H．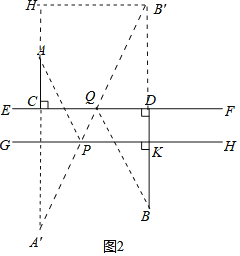

则此时AP+PQ+QB的值最小．
根据对称的性质可知：PA=PA′，QB=QB′，
∴PA+PQ+QB=PA′+PQ+QB′=A′B′，
∴PA+PQ+PB的最小值为线段A′B′的长，
在Rt△A′B′H中，∵HB′=CD= ，

HA′=DB′+CA′=7+6=13，
∴A′B′= ，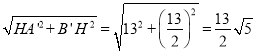
∴AP+PQ+QB的最小值为．