题目内容
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
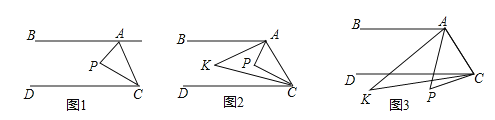
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,则∠APC= .
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系为 .
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
【答案】(1)80°;(2)∠AKC=![]() ∠APC;(3)∠AKC=
∠APC;(3)∠AKC=![]() ∠APC.
∠APC.
【解析】试题分析:(1)过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据![]() 进行计算即可;
进行计算即可;
(2)过K作KE∥AB,根据KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义,得![]() 进而得到
进而得到![]()
(3)过K作KE∥AB,根据KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠AKE∠CKE=∠BAK∠DCK,同理可得,∠APC=∠BAP∠DCP,再根据角平分线的定义,得出![]() 进而得到
进而得到![]()
试题解析:(1)如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴![]()
(2) ![]()

理由:如图2,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴![]()
∴![]()
(3) ![]()
理由:如图3,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK
∴∠AKC=∠AKE∠CKE=∠BAK∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴![]()
∴![]()