Question

I．计算：（

x+3

x2-3x

-

x-1

x2-6x+9

）÷

x-9

x

．
II．解分式方程：

x-2

x+2

-

16

x2-4

=

x+2

x-2

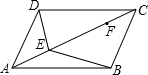
III．如图，?ABCD中，点E、F在对角线AC上，且AE=CF，请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想证明它和图中已有的某一线段相等．（只须证明一组线段即可．）
（1）连接

 

；（2）猜想

 

=

 

；（3）写出证明过程．

Answer 1

分析：I、先将括号里面的进行通分，然后再进行分式的除法运算即可得出答案．
II、先移项，然后根据分子相等、分母不等于零即可解出x的值．
III、可连接BF，通过证明△ADE≌△CBF得出BF=DE．

解答：解：I、原式=（

x2-9

x(x-3)2

-

x2-x

x(x-3)2

）×

x

x-9

=

x-9

x(x-3)2

×

x

x-9

=

1

(x-3)2

．

II、原方程可化为：

x-2

x+2

-

x+2

x-2

=

16

x2-4

，即

-8x

x2-4

=

16

x2-4

，
∴-8x=16，
解得：x=-2．
当x=-2时，分母x²-4=0，无意义，
故方程无解．

III、连接BF，
在△CBF和△ADE中，

CF=AE ∠DAE=∠BCF AD=CB

，
∴△CBF≌△ADE，
∴BF=DE．

点评：本题考查了分式的混合运算及平行四边形的性质，考查的知识点比较多，难度一般，解答本题要细心运算，减少计算失误，另外第三问的解答中属于开放题，要灵活解答．