题目内容
 如图,M是△ABC的BC边上的一点,AM的延长线交△ABC的外接圆于D,已知:AM=9cm,BD=CD=6cm,
如图,M是△ABC的BC边上的一点,AM的延长线交△ABC的外接圆于D,已知:AM=9cm,BD=CD=6cm,
(1)求证:BD2=AD•DM;
(2)求AD之长.
(1)证明:∵BD=DC,
∴∠BAD=∠DAC;
又∵∠DBC=∠DAC,
∴∠DBC=∠BAD,
又∵∠BDA=∠MDB,
∴△ABD∽△BMD,
∴
∴BD2=AD•DM.
(2)解:由(1)得62=AD(AD-9),
AD2-9AD-36=0,
AD=12,AD=-3,(舍去)
∴AD的长是12cm.
分析:(1)将所求的乘积式化为比例式,然后证线段所在的三角形全等即可,即证△BDM∽△ADB.
(2)用AD表示出DM,然后将BD的值代入(1)题的结论中,即可求得AD的长.
点评:此题主要考查的是圆周角定理和相似三角形的性质判定和性质.
∴∠BAD=∠DAC;
又∵∠DBC=∠DAC,
∴∠DBC=∠BAD,
又∵∠BDA=∠MDB,
∴△ABD∽△BMD,
∴

∴BD2=AD•DM.
(2)解:由(1)得62=AD(AD-9),
AD2-9AD-36=0,
AD=12,AD=-3,(舍去)
∴AD的长是12cm.
分析:(1)将所求的乘积式化为比例式,然后证线段所在的三角形全等即可,即证△BDM∽△ADB.
(2)用AD表示出DM,然后将BD的值代入(1)题的结论中,即可求得AD的长.
点评:此题主要考查的是圆周角定理和相似三角形的性质判定和性质.

练习册系列答案
相关题目
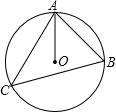 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
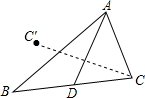 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=