题目内容
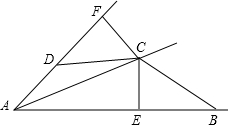如图，已知AC平分∠BAD，CF⊥AD于F，CE⊥AB于E，DC=BC．
求证：△CFD≌△CEB．
解：∵AC平分∠BAD，CE⊥AB，CF⊥AD，
∴CE=CF（角平分线上的点到角的两边的距离相等）；
在Rt△BCE和Rt△DCF中，
∵
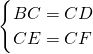
∴Rt△BCE≌Rt△DCF（HL）．
分析：根据角平分线上的点到角的两边的距离相等可得CE=CF，利用“HL”即可证明△BCE和△DCF全等．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定．
∴CE=CF（角平分线上的点到角的两边的距离相等）；
在Rt△BCE和Rt△DCF中，
∵
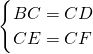
∴Rt△BCE≌Rt△DCF（HL）．
分析：根据角平分线上的点到角的两边的距离相等可得CE=CF，利用“HL”即可证明△BCE和△DCF全等．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
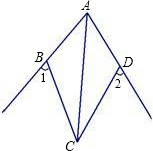
如图，已知AC平分∠BAD，∠1=∠2，求证：AB=AD．
2、如图，已知AC平分∠BAD，∠1=∠2，AB=DC=3，则BC=
如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD．