Question

【题目】如图，已知抛物线经过点A（﹣1，0）、B（3，0）、C（0，3）三点．

（1）求抛物线的解析式．
（2）点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，请用m的代数式表示MN的长．
（3）在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．

Answer 1

【答案】
（1）解：设抛物线的解析式为：y=a（x+1）（x﹣3），则：

a（0+1）（0﹣3）=3，a=﹣1；

∴抛物线的解析式：y=﹣（x+1）（x﹣3）=﹣x2+2x+3

（2）解：设直线BC的解析式为：y=kx+b，则有：

，

解得 ；

故直线BC的解析式：y=﹣x+3．

已知点M的横坐标为m，MN∥y，则M（m，﹣m+3）、N（m，﹣m2+2m+3）；

∴故MN=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m（0＜m＜3）．

（3）解：如图：

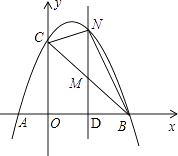
∵S△BNC=S△MNC+S△MNB= MN（OD+DB）= MNOB，

∴S△BNC= （﹣m2+3m）3=﹣ （m﹣ ）2+ （0＜m＜3）；

∴当m= 时，△BNC的面积最大，最大值为 ．

【解析】（1）观察已知点坐标的特点，可设函数解析式为两根式，将点的坐标代入即可求出函数解析式。
（2）先求出直线BC的函数解析式，抓住MN∥y轴，点M是线段BC上，点N在抛物线上，告诉了点M的横坐标为m，因此可以表示出点M、N的坐标，就可以用m的代数式表示MN的长．
（3）先求出S△BNC与x的函数关系式，再求出此二次函数的顶点坐标，即可求出结果。