题目内容
如图所示,AB为⊙O的直径,P为AB延长线上一点,PD切⊙O于C,BC和AD的延长线相交于点E,且AB=AE。 (1)求证: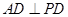 (2)若圆的半径为1,△ABE是等边三角形,求BP的长.
(2)若圆的半径为1,△ABE是等边三角形,求BP的长.
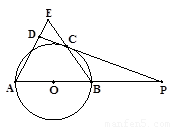
【解析】(1)连OC,根据切线的性质得到OC⊥PD,又AB=AE,OC=OB,则∠2=∠E,∠1=∠2,得到∠1=∠E,则OC∥AE,即可得到结论;
(2)根据等边三角形的性质得∠A=60°,则∠COB=60°,则∠P=30°,再根据含30°的直角三角形三边的关系得到OP=2OC=2,从而求出BP
【答案】
(1)证明:连OC,如图,
∵PD切⊙O于C,
∴OC⊥PD,
∵AB=AE,
∴∠2=∠E,
而OC=OB,
∴∠1=∠2,
∴∠1=∠E,
∴OC∥AE,
∴AD⊥PD;
(2)解:∵△ABE是等边三角形,
∴∠A=60°,
∴∠COB=60°,
而∠OCP=90°,OB=OC=1,
∴∠P=30°,
∴OP=2OC=2,
∴BC=2-1=1.

练习册系列答案
相关题目
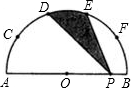 如图所示,AB为半圆O的直径,C、D、E、F是
如图所示,AB为半圆O的直径,C、D、E、F是
 如图所示,AB为圆O的弦,OC垂直AB于点C,OC=3,若圆O的半径为5,则弦AB的长为
如图所示,AB为圆O的弦,OC垂直AB于点C,OC=3,若圆O的半径为5,则弦AB的长为 (2013•孝南区一模)已知,如图所示,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交于⊙O于点E,∠BAC=45°,给出以下四个结论:
(2013•孝南区一模)已知,如图所示,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交于⊙O于点E,∠BAC=45°,给出以下四个结论: 如图所示,AB为⊙O的直径,AC为弦,OD∥BC交AC于D,若AB=20cm,∠A=30°,则OD=
如图所示,AB为⊙O的直径,AC为弦,OD∥BC交AC于D,若AB=20cm,∠A=30°,则OD= 如图所示,AB为⊙O的直径,D为
如图所示,AB为⊙O的直径,D为