Question

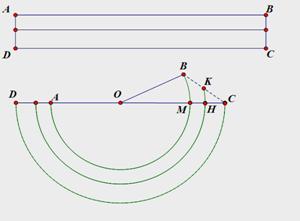
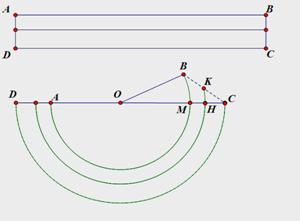
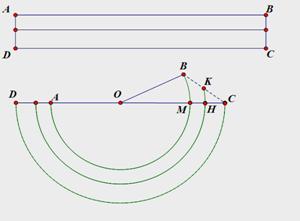
如图，矩形ABCD为一本书，AB=12π,AD=2，当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧)，如第一张纸AB对应为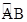，最后一张纸CD对应为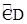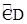（为半圆），

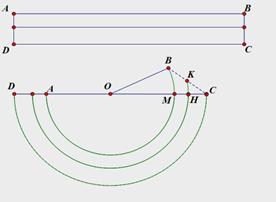
（1）连结OB，求钝角∠AOB=          ；

（2）如果该书共有100张纸，求第40张纸对应的弧超出半圆部分的长.

 

Answer 1

【答案】

（1）144°；（2）.

【解析】

试题分析：（1）每张纸的长度相等，即上图中AB=CD=12π，∵上图中CD=下图中，∴下图中=πOD，得OD=12，OA=ODAD=10. 由=12π=10θ，得θ==216°，∴∠AOB=360°216°=144°. （2）求出半径为OH的圆的半圆周长，由=半径为OH的圆的半圆周长即得.

试题解析：（1）144°.

（2）设第40张纸对应的弧超出半圆部分为，

∵MC=AD=2，，得MH=0.8. ∴OH=10.8.

∵半径为OH的圆的半圆周长＝OHπ＝10.8π，

∴.

考点：弧长的计算.