Question

已知实数x，y，z满足x+y+z=5，xy+yz+zx=3，则z的最大值是

1. A.
   3
2. B.
   4
3. C.
   
4. D.
   

Answer 1

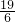
D
分析：把x，y看成是一元二次方程的两个实数根，根据根与系数的关系列出一元二次方程，然后由判别式得到z的取值范围，求出z的最大值．
解答：∵x+y=5-z，xy=3-z（x+y）=3-z（5-z）=z²-5z+3，
∴x、y是关于t的一元二次方程t²-（5-z）t+z²-5z+3=0的两实根．
∵△=（5-z）²-4（z²-5z+3）≥0，即3z²-10z-13≤0，
（3z-13）（z+1）≤0．
∴-1≤z≤，
当 x=y=时，z=．
故z的最大值为 ．
故选D．
点评：本题考查的是一元二次方程根与系数的关系，根据根与系数的关系列出一元二次方程，然后由判别式求出z的取值范围，确定z的最大值．